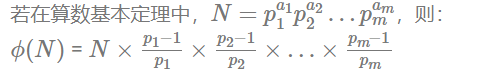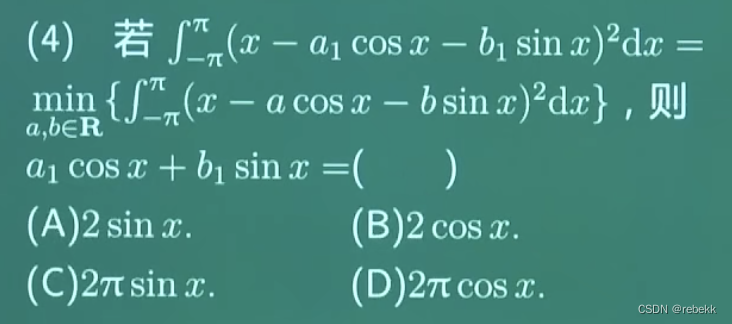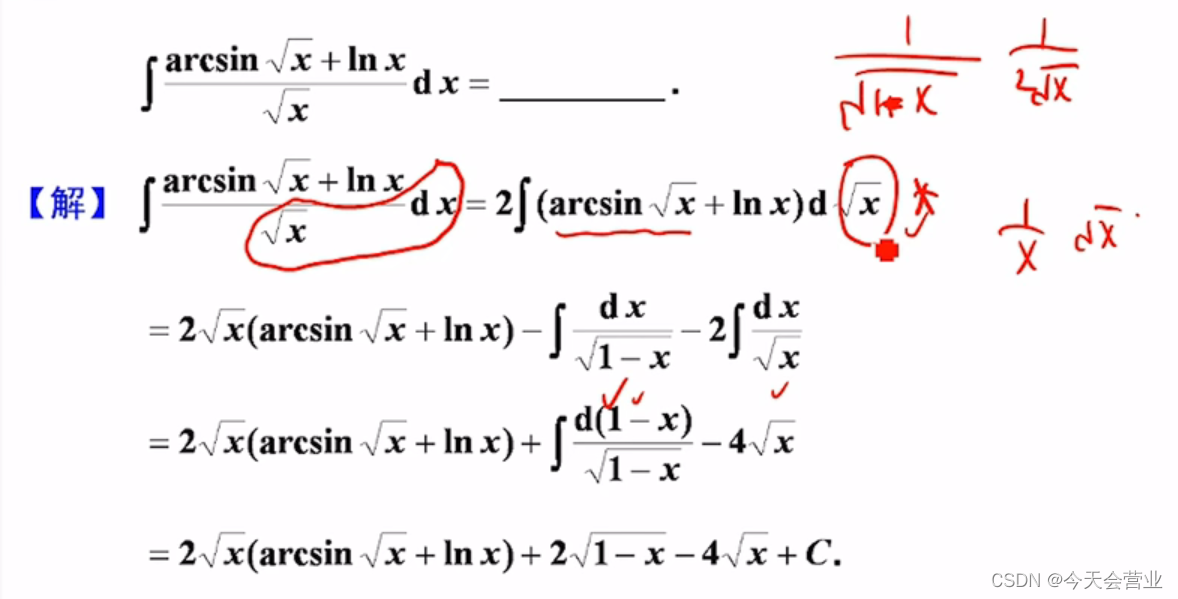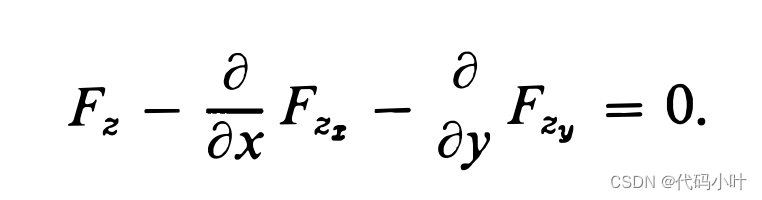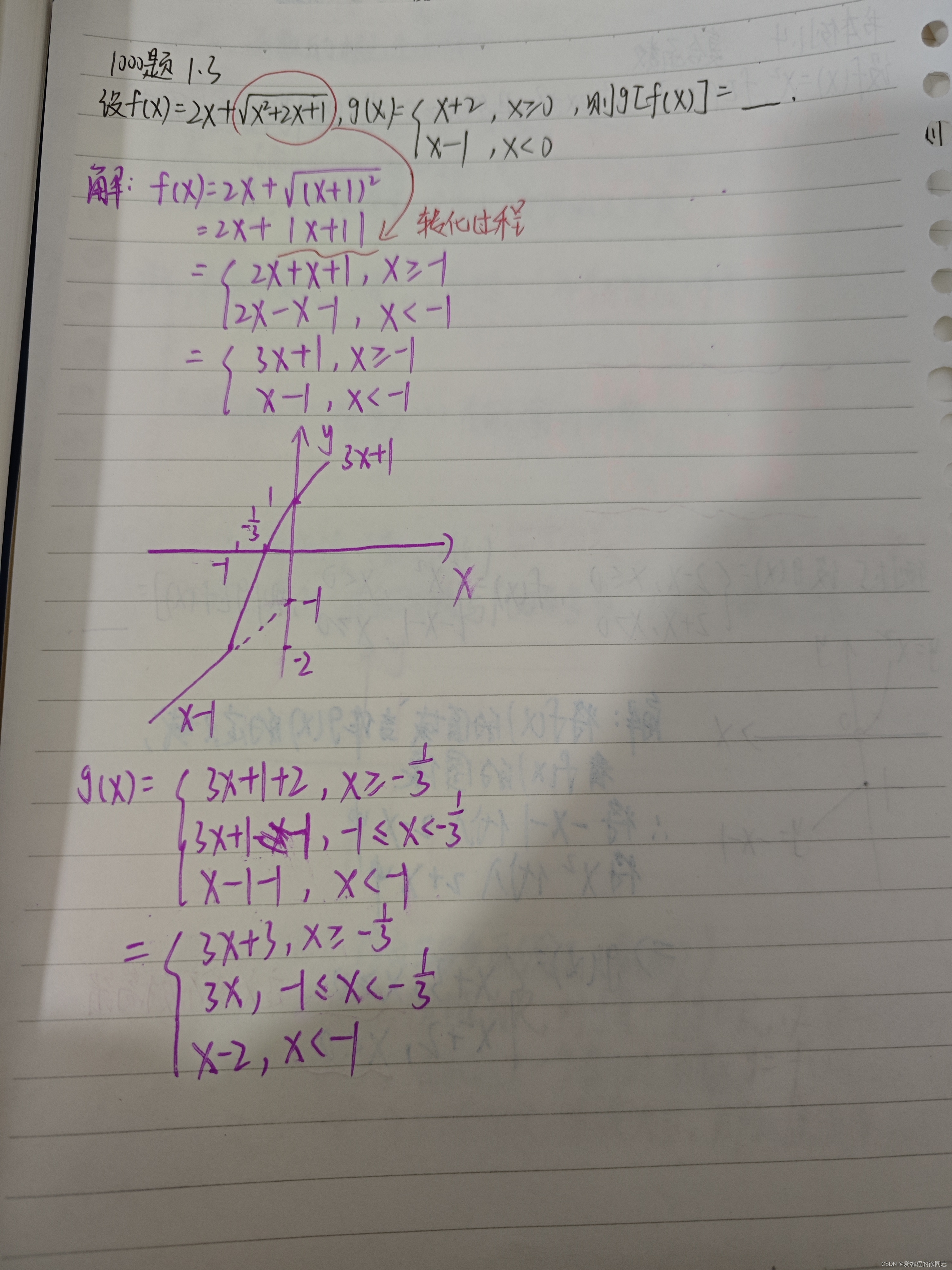英语
机器视觉
pcb布局
htap
PID
SSM就业管理
电池
医学
JDK17.0.2
996
银行家算法
java-ee
初识SpringBoot
贝叶斯网络
dubbo
ai
智慧
mes
SecOC
改进粒子群优化算法
数学
2024/4/11 15:17:223.8每日一题(凑微分求不定积分)
方法一:通过化sin2x凑dcosx的平方 方法二:通过一个sinx和一个2cosx凑dcosx的平方 先化sinx为dcosx;再把 cosx 看成是 u 通过2ududu的平方的思想化出 dcosx的平方
二元回归方程中的斜率b与协方差的关系
最近在《Causal inference in Statistics:A primer》(统计因果推理入门)的第一章1.3.10中看到这样一句话,即若Y关于X的回归方程为yabx,则斜率b可以用协方差计算,即: bRXYσXYσX2b R_{XY}\frac{σ_{XY}}{σ_{X}^2} bR…
关于欧拉函数积性的问题
Proposition 若(m,n)1\text{Proposition 若}(m,n)1Proposition 若(m,n)1,那么φ(mn)φ(m)φ(n).\varphi(mn)\varphi(m)\varphi(n).φ(mn)φ(m)φ(n). 首先中国剩余定理断言 x≡a(modm)x≡b(modn)\begin{array}{cc}x\equiv a& \pmod{m}\\x\equiv b& \pmod{n}\en…
讲解一些复变函数的基础概念
可以对实数域做一个推广复数域,于是获得一个比较好的性质.我们把多项式函数的f(x)x21f(x)x^21f(x)x21的根i−1i\sqrt{-1}i−1添加入实数域,得知CR[i]≅R2CR[i]\cong R^2CR[i]≅R2. 在复数域上的加减乘除是很简单的,并且由欧拉公式得到的eiθe^{i\theta}eiθ也能够应用到这个域…
[JZOJ6045]【NOI2019模拟2019.3.7】能量
Description
有n个随机变量xi,第i个在[li,ri]内均匀随机,问max((∑xi)^k,a ^k)的期望 n<50,-2000<li<ri<2000
Solution
先把li累加起来,每个xi变成在[0,len[i]]内均匀随机 设Fi(x)F_i(x)Fi(x)表示∑j1ixj\sum_{j1}^{i}xj∑j…
杭电ACM——1018,Big Number(思维)
数学题,用取对数函数就好。 突破口: 公式:log(i1)!log(i1)log(i)!; 遍历1~1e7内所有数的阶乘,记录下其对于10的对数log10(i),最终输出的数要1。 代码如下:
#include<cstdio>
#include<cmath>
…
牛客练习赛33 A,B,C,D,E,F
A - tokitsukaze and Counting
求[L,R][L,R][L,R]之间有多少个数能被xxx整除. 考虑前缀[1,L][1,L][1,L],一共有L/xL/xL/x个数字是xxx的倍数.签到题不多讲…
#include <cstdio>
int main(){int T;scanf("%d",&T);while(T--){long long L,R,x;scanf("…
2019 BUPT Winter Training #1 div.2
1100C - A - NN and the Optical Illusion
难度: 初中几何 一道几何题,根据几何关系: RRrsinπn.\frac{R}{Rr}\sin \frac{\pi}{n}. RrRsinnπ.
#include <cstdio>
#include <cmath>
const double PIacos(-1.0);
int main(){int n;double r;scanf("%d%…
4.1每日一题(多元函数微分:偏导数判定(链导法、定义、先代后求))
链导法:如果每一层复合都可导(即在判断点要可导),则复合函数一定可导;如果中间层有不可导,就不方便使用链导法了(在(0,0)点不可导)
当链导法不好用时应该直接…
可能是入门高阶数学的好通道 —— 很直观易记,又很难判断的真假的数学命题们
1. 有理数和无理数
实数轴上,2.0右侧的第一个实数b,b是无理数;(么?) 2. 点的个数 实数轴上0.0到2.0之间距离,是0.0到1.0之间距离的2倍,所以,显然,0.0到2.0之…
HDU2086, A1=?(数学)
数学推导过程: https://blog.csdn.net/yexiaohhjk/article/details/50229533 代码如下:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cctype>
#include<queue>
using na…
3.18每日一题(奇偶性、奇偶性的平移、几何意义、配方、换元)
解法一:先配方,再用三角函数换元(看见根号一般用三角函数),看见对称区间联想奇偶性,最后再用公式
解法二: 利用奇偶性的平移,令(x-1) t ,对应的区…
数学回味系列之14 - 汉诺塔
问题提出: 古代有一个梵塔,塔内有3个座 A、B、C。 A座上有64个圆盘,盘子大小不等,大的在下,小的在上。 有一个和尚想把这64个盘子从A座移动到C座,每次只能移动一个圆盘,并在移动过程中始终保持大…
3.2每日一题(定积分求抽水做工问题)
1、画图,把题目的容器画出来:球形容器,半径为R
2、根据容器的形状进行分析: 抽水的实质是不同深度的水抽出去走的位移是不一样的>抽水的过程 : (1)先考虑深度为 x到xdx 的薄层水抽出去做多少…
抽象代数基础 群论(1)
definitiondefinition群:一个群是一个集合G带有一个二元运算, 这个二元运算一般称为乘法⋅:GG→G⋅:GG→G,将(a,b)记作a⋅b或者ab(a,b)记作a⋅b或者ab,称为积。 群的判定:①运算⋅⋅满足结合律;②运算的群…
LeetCode 231. 2的幂
原题目:https://leetcode-cn.com/problems/power-of-two/ 代码:
如果是2的幂次方,那么就可以表示成2的乘积。所以不断除以2就可以了,如果最后得到的因子是1那么就返回真 代码:
class Solution {
public:bool isPower…
LeetCode 367. 有效的完全平方数
原题目:https://leetcode-cn.com/problems/valid-perfect-square/ 思路:
根据小学的知识,完全平方数可以拆分为一系列奇数的加和,例如:
25 1 3 5 7 9 代码:
class Solution {
public:bool isPerfec…
2019牛客暑期多校训练营(第一场) Random Point in Triangle (推结论或随机数猜结论)
正解证明:https://www.cnblogs.com/WAautomaton/p/11211864.html
(着实看不懂。。。。。太菜了。)
当然也可以随机数确定点P,多随机几个点,便可以得到36E是其面积的10点多倍。因为是整数,11倍即可。
#in…
【经典专题】寻找质数——巧妙的埃氏筛和线性筛
很经典的题目:给出nnn,统计 [2,n)[2,n)[2,n) 中质数的数量 Demo1:input 10,output 4 Demo2:input 100,output 25 暴力枚举
首先,复习一遍质数的定义:在大于1的自然数中,…
对于高等代数一下比较基础的概念的认识
至多是一次齐次方程的方程组称为线性方程组,每个方程组可以表示为如下形式: m∑j1ajxjbi(i1,2,...,n) 其中将aij称为系数,将xj称为未知量,bi称为常数项. 把上面的n元线性方程组写成“表格”也就是矩阵形式: ⟮a11a12⋯a1mb1a21a22⋯a2mb2⋮⋮⋱⋮⋮an1an2⋯anmbn⟯\left\lg…
2023年高考真题练习
在直角坐标系 x O y xOy xOy中,点 P P P到 x x x轴的距离等于点 P P P到点 ( 0 , 1 2 ) (0,\dfrac 12) (0,21)的距离,记动点 P P P的运动轨迹为 W W W (1)求 W W W的方程 (2)已知矩形 A B C D ABCD ABCD有…
关于同构关系的一些证明(1)
定义一种集合乘法XY{xy∣x∈X,y∈Y}XY\{xy|x\in X,y\in Y\}XY{xy∣x∈X,y∈Y}. 那么我们可以看见若H⩽GH\leqslant GH⩽G,则HH{hh′∣h,h′∈H}{h∣h∈H}HHH\{hh'|h,h'\in H\}\{h|h\in H\}HHH{hh′∣h,h′∈H}{h∣h∈H}H. 特别的,若集合中只有一个元素,那么可…
数学回味系列之22 - 四方定理
问题提出: “四方定理” 是数论中著名的一个定理,指 所有自然数至多只要用四个数的平方和就可以表示。 解题思路: 比较简单,直接给出代码: #include<stdio.h>
#include<stdlib.h>
#include<conio.h>…
LeetCode 537. 复数乘法
原题目:https://leetcode-cn.com/problems/complex-number-multiplication/ 思路:
关键在于提取string中的实数和虚数。可以使用c中的sscanf。 代码;
class Solution {
public:string complexNumberMultiply(string a, string b) {int a1,a2,b1,b2;ssc…
LeetCode 279. Perfect Squares
原题目:https://leetcode-cn.com/problems/perfect-squares/ 思路一:
进行广度优先遍历,先创建完全平方数数组sq,对于一层中的元素依次和数组sq的元素进行比较。
1、如果元素等于sq的元素:说明找到了答案
2、如果元…
数学回味系列之20 - 常胜将军
问题提出: 规则:A B 两人玩取火柴的游戏,共有 21 根火柴。 每人每次最多取 4 根,最少取 1 根。取到最后一根火柴的玩家算输。 如何保证某一玩家每次都赢? 解题思路: 常胜将军 是 取火柴游戏 的一个特例。 如…
LeetCode 面试题 01.07. 旋转矩阵
原题目:https://leetcode-cn.com/problems/rotate-matrix-lcci/ 思路: 先上下翻转,再求转置
代码:
python版本
matrix[::] zip(*matrix[::-1])
c版本
class Solution {
public:void rotate(vector<vector<int>>…
Codeforces Educational Codeforces Round 56 (Rated for Div. 2) 1093G. Multidimensional Queries
有一kkk维点序列。 求[l,r][l,r][l,r]之间Manhattan\text{Manhattan}Manhattan距离最大的点。要求点修改区间查询。 解:每维的坐标分解如下: ∣aj−bj∣aj−bjorbj−aj,j1,2,...,k|a_{j}-b_j|a_{j}-b_{j}\ or\ b_{j}-a_{j},j1,2,...,k∣aj−bj∣aj−bj or b…
简单组合学(4) Polya计数定理(2)
Definition Definition 群G⩽Sn的k−G⩽Sn的k−不动置换类ZkZk称作使akak不改变位置的置换集合,它是群GG的子群.例如群G={e,(1 2),(3 4),(1 2)(3 4)}" role="presentation" style="position: relative;">G={e…
LeetCode 264. 丑数 II
原题目:https://leetcode-cn.com/problems/ugly-number-ii/ 思路:
我们分析得到,每次新的丑数都是小丑数乘以(2、3、5),我们只需要选择其中最小的,并且用三个指针记录2、3、5对应小丑数的索引。…
图论的一些简单命题的证明
Proposition 1 如果GGG是简单图,那么: ϵ(G)⩽{v(v−1),if vis directed.12v(v−1),if vis undirected.\epsilon(G)\leqslant \left\{\begin{array}{ll} \displaystyle v(v-1)&,\text{if }v \text{ is directed}.\\ \displaystyle \frac{1}{2}v(v-1)&,\text{if…
HDU5605——数学题(三角函数的应用)
题目描述: geometry
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Submission(s): 356 Accepted Submission(s): 269 Problem DescriptionThere is a point Pat coordinate (x,y).A line goes through the poin…
LeetCode 263. 丑数
原题目:https://leetcode-cn.com/problems/ugly-number/ 思路:
丑数可以表示成2,3,5的乘积,所以我们在num可以整除2,3,5的情况下,不断整除。如果最后得到的因子是1,那么就是丑数。 代码;
class Solution {
public:bo…
数学物理学家心中的十大最美方程
“你认为最美的数学、物理方程是什么?”当代十位大数学家、物理学家给出了他们自己的回答。这些回答构成了大雅之美(The Concinitas Project)的十篇文章。我们为读者带来这些大师对自己眼中最美方程的精彩解读。
1.指标定理
撰文 阿蒂亚爵士…
任意分圆环下的 RLWE:如何产生正确的噪声分布
参考文献:
[Con09] Conrad K. The different ideal[J]. Expository papers/Lecture notes. Available at: http://www.math.uconn.edu/∼kconrad/blurbs/gradnumthy/different.pdf, 2009.[LPR10] Lyubashevsky V, Peikert C, Regev O. On ideal lattices and learn…
markdown写累计求和的数学公式
DAUNAN∑i1NAN−1∗RiDAU_NA_N\sum_{i1}^NA_{N-1}*R_iDAUNAN∑i1NAN−1∗Ri
$DAU_NA_N\sum_{i1}^NA_{N-1}*R_i$然后自己找规律改就行
数学回味系列之21 - 角谷猜想
问题提出: 角谷猜想 又称 冰雹猜想。 对于 一个正整数n: 1)如果 n 为偶数,就将它变为 n/2; 2)如为奇数,则将它 乘3加1(3n1); 不断重复这样的运算,…
七夕特别篇 | 浪漫的Bug
文章目录 前言一、迷失的爱情漩涡(多线程中的错误同步)1.1 Bug 背景1.2 Bug 分析1.3 Bug 解决 二、心形积分之恋(心形面积计算中的数值积分误差)1.1 Bug 背景1.1.1 背景1.1.2 数学模型 1.2 Bug 分析1.2.1 初始代码1.2.2 代码工作流…
LeetCode 2485. 找出中枢整数
【LetMeFly】2485.找出中枢整数
力扣题目链接:https://leetcode.cn/problems/find-the-pivot-integer/
给你一个正整数 n ,找出满足下述条件的 中枢整数 x :
1 和 x 之间的所有元素之和等于 x 和 n 之间所有元素之和。
返回中枢整数 x 。…
【剑指offer】数字序列中某一位的数字
🔥题目
数字序列为:01234567891011121314151617181920212223242526272829…
输入:13 输出:1
输入:200 输出:0 ☘️解析
比较有难度的数学问题。请耐心看完下面的讲解 >_< !
首先&…
【经典专题】分割整数得到最大乘积——剪绳子问题
问题引入
给你一根长度为 n 的绳子,请把绳子剪成整数长度的若干段,然后把各段长度相乘,能得到的最大乘积是多少?(注:长度n至少为2,你至少要剪一次)
举个例子:
绳子长度…
数论 整除理论(1)
Problem Problem 设奇数n>1n>1,证明:nn是素数的充分必要条件是n" role="presentation" style="position: relative;">nn不能表为三个或三个以上的连续正整数之和。 解: 必要性: 设自然数前缀…
PLONK电路如何构造,PLONK例子
文章目录个人总结如何理解电路Gate ConstraintsCopy constraints多项式承诺参考资料个人总结
PlonK相比起之前的zkSNARK协议来说,主要区别在于三点,
1-首先是在将电路解释为多项式的时候,SNARK协议一般采用R1CS到QAP的做法,最后…
C++二分查找算法:阶乘函数后 K 个零
涉及知识点
二分查找 数学
题目
f(x) 是 x! 末尾是 0 的数量。回想一下 x! 1 * 2 * 3 * … * x,且 0! 1 。 例如, f(3) 0 ,因为 3! 6 的末尾没有 0 ;而 f(11) 2 ,因为 11! 39916800 末端有 2 个 0 。 给定 k&a…
机器学习中的数学(1)-回归(regression)、梯度下降(gradient descent)
版权声明: 本文由LeftNotEasy所有,发布于http://leftnoteasy.cnblogs.com。如果转载,请注明出处,在未经作者同意下将本文用于商业用途,将追究其法律责任。 前言: 上次写过一篇关于贝叶斯概率论的数学,最…
5.1每日一题(无穷级数敛散性的判断:莱布尼兹准则、p级数、绝对收敛、条件收敛、比较法/比较法的极限形式)
莱布尼兹准则:(1)单调递减;(2)极限 -> 0
绝对收敛:级数的绝对值收敛
条件收敛:级数的绝对值发散
p级数的次幂 <1 时发散 ;>1时收敛
2019牛客暑期多校训练营(第一场) B Integration (公式推导)
高中都学过等差数列的裂项吧,这里就是用裂项来化简式子,把相乘的式子化为相减的式子,问题就得到简化。假设n3,数值分别为a,b,c。推导过程请看下图: 注意有些相乘的地方会溢出,时刻取…
算法竞赛中的常用JAVA API :Math类
Math类包含了一些常用的数学方法,在java.lang.*包内。 (不能用于大数类,大数类请参见备战蓝桥杯java(五):算法竞赛中的常用API :大数类) 了解其他JAVA 常用API和算法点这里 >> https://blog.csdn.net/GD_ONE/art…
趣味数学题存疑待证1
原文出自:球面上随机 N 个点在同一个半球上的概率
要求任意N个点,全在同一个半球上的概率,我们需要构造使得分母为有限的样本集合,分子则为有N个点在同一半球的情况集
首先对任意N个点取其对称点使得可划分点为2N,在…
FHEW 和 TFHE 的统一框架:标准化 FHE
参考文献:
[GHS12] Gentry C, Halevi S, Smart N P. Better bootstrapping in fully homomorphic encryption[C]//International Workshop on Public Key Cryptography. Berlin, Heidelberg: Springer Berlin Heidelberg, 2012: 1-16.[GHPS12] Gentry C, Halevi S,…
Leetcode刷题【每日n题】(3)
🎵今日诗词🎵 桃花潭水深千尺,不及汪伦送我情。 ——李白《赠汪伦》 目录
1.题目一
2.思路分析
3.代码实现
4.题目二
5.思路分析
6.代码实现 1.题目一 9. 回文数 给你一个整数 x ,如果 x 是一个回文整数,返回 tr…
【算法基础 数学】快速幂
题目描述
给定 n n n组 a i , b i , p i a_i,b_i,p_i ai,bi,pi,对于每组数据,求出 a i b i m o d p i a_i^{b^i}~mod~p_i aibi mod pi 的值。
样例
输入样例:
2
3 2 5
4 3 9输出样例:
4
1快速幂解决的问题
用来…
简单的无理函数的不定积分
前置知识:
直接积分法有理函数的不定积分
简单的无理函数的不定积分
对无理函数积分的基本方法就是通过换元将其化为有理函数的积分。下面讲讲几类无理函数积分的求法。
注: R ( u , v ) R(u,v) R(u,v)是由 u , v u,v u,v与常数经过有限次四则运算得…
EXCEL数据计算分析功能助力PID闭环控制优化
EXCEL大家并不陌生,这篇博客记录汇总利用EXCEL进行工作分析的一些技巧,专栏也会持续更新,感谢大家关注评论。首先介绍下工控上用的比较多的模拟量采集,模拟量采集的数学基础大家可以查看下面的博客:
PLC模拟量输出 模拟量转换FC S_RTI_博图模拟量输出指令_RXXW_Dor的博客…
数学回味系列之12 - 龟兔赛跑问题
问题提出: 乌龟与兔子进行赛跑,乌龟每分钟可以前进3米,兔子每分钟前进9米; 兔子嫌乌龟跑得慢,觉得肯定能跑赢乌龟,于是,每跑10分钟回头看一下乌龟: a)若发现自己超过乌龟…
数学回味系列之13 - 杀猪问题
问题提出: 有 N 头猪 和 一个变态的屠夫; 屠夫就喜欢杀单数位置上的猪,一次杀完之后,将剩下的猪按照原来的相对位置,重新排列; 按照约定,最后一头猪(取名Lucky)将会被送到…
线性代数的本质(笔记一)
注:本篇笔记来源于《线性代数的本质》一课程。
写在前面
本课程主要通过几何来了解线性代数
1. 向量
对于向量有三种观点:
物理学 具有大小和方向计算机 数组,列表数学 概括前面两者,只要保证向量的加法和数乘有意义即可。…
[补题]2018 BUPT Winter Training #1 div.1
A,B,D,F看下面: https://blog.csdn.net/Myriad_Dreamin/article/details/79209441 C看这里: https://blog.csdn.net/Myriad_Dreamin/article/details/79349060
CodeForces - 697D - E - Puzzle
我们知道期望拥有线性性,所以假设iii是待求顶点,preprepre是父亲数组,sizsizsiz是…
初中数学:几何题的相关解题原则总结
一、多问类型的几何题
我们做题,应该都遇到过这类几何题目,就是,三个小问,每个小问对应一个几何图像,而且,渐渐复杂。这种题目,大多数有一个变化的条件,比如,动点、角度…
1.填空题 进制转换Oct.2023
原题
部分可能会有用处的知识: p p p进制转十进制: 假设有一个 p p p进制数,个位是 a 0 a_0 a0,向高位依次是 a 1 , a 2 , . . . , a n a_1,a_2,...,a_n a1,a2,...,an,向低位依次是 b 1 , b 2 , b 3 , . . . …
Annual summary(年度总结)--数据总结篇
《大数据时代》大数据正把我们变成新的物种。首先,大数据改变了我们的思维方式,让我们从因果关系的串联思维变成了相关关系的并联思维。第二,大数据改变了我们的生产方式,物质产品的生产退居次位,信息产品的加工将成为…
入门数学----我真的学过数学了吗
一、我会加法公式了吗? 二、这是乘法吗? 三、排列
原来我连排列也没有从电脑里试过它的真相! 四、排列组合 在排列组合的世界里,我需要多学习和记录啊!太神奇了!
简单组合学(3) Polya计数定理(1)
简单组合学(3)
Polya计数定理(1) 1 引言
在固定的正六边形顶点上摆放一个黑球、一个红球和四个白球的方法有多少种,读过初中的人一定能够轻而易举地得到答案,读过小学的人也能够枚举所有结果,答案是65306530种. 但是如果不固定呢?学过高中化学的应该有所印象,一共…
高等近世代数笔记(1) 置换与群
(Definition)设α∈Sn,且α∏i1tβi(βi∈Sn)是分解为不相交轮换的完全轮换分解:定义sgn(α)(−1)n−t.(Definition)设α∈Sn,且α∏i1tβi(βi∈Sn)是分解为不相交轮换的完全轮换分解:定义sgn(α)(−1)n−t.(Theorem)∀α,β∈Sn,sgn(αβ)sgn(α)sgn(β).(Theorem)∀α,β∈S…
BUPT kamiyoru's training #2 codeforces#485div.2
A - Infinity Gauntlet
签到题,就不多扯了。
#include <iostream>
#include <string>
#include <map>
using namespace std;
char str[10][10]{"","Power","Time","Space","Soul","Re…
杭电ACM——2058
看题: Given a sequence 1,2,3,…N, your job is to calculate all the possible sub-sequences that the sum of the sub-sequence is M.
Input contains multiple test cases. each case contains two integers N, M( 1 < N, M < 1000000000).input ends w…
伊恩·斯图尔特《改变世界的17个方程》傅里叶变换笔记
主要是课堂的补充(yysy,我觉得课堂的教育模式真有够无聊的,PPT、写作业、考试,感受不到知识的魅力。 它告诉我们什么? 空间和时间中的任何模式都可以被看作不同频率的正弦模式的叠加。 为什么重要? 频率分量…
抽象代数基础 环论(1)
首先一个环乘法满足半群的性质: 1.封闭 2.满足结合律 其次一个环加法满足阿贝尔群的性质: 若环乘法满足交换律,半群含幺,称其为交换环. 若交换环满足乘法消去律,称其为整环. Example RExample R是整环,找出两个函数f,g∈I(R),f≢0,g≢0f,g∈I(R),f≢0,g≢0但fg≡0fg≡…
一个有趣的组合恒等式证明(复旦数学考试第7题)
试证:∑jkn0⩽j<k⩽n(2jj)(2kk)4n.∑jkn0⩽j<k⩽n(2jj)(2kk)4n.证明1: 考虑一个母函数f(x)11−4x((1−4x)−12)2f(x)11−4x((1−4x)−12)2(观察左式,它是一个卷积形式,因而如此构造). 11−4x∑n0∞4nxn11−4x∑n0∞4nxn,且: ((1−4x)−12)2∑n0∞(∑jkn(−12j)(−12k)…
杭电ACM——2051,十进制转二进制(正整数)
十进制正整数n转二进制,只要将n取余2,将其得到的余数存入数组,再将n/2,不断重复操作直到n0,最终将数组元素逆序输出即可。 代码如下:
#include<cstdio>
using namespace std;
int main()
{int a[105…
2.27每日一题(定积分求面积,旋转体体积)
1、遇到求面积、定积分的问题,先画图: (1)抛物线(可正可负,所以抛物线函数需要有 a 变量) (2)过两个点
2、定积分求面积有三种情况对应三条公式: ࿰…
北航OJ 0031~0037 2015级C++第二次上机
0032 - A - cool_breeze的袜子 开心的天数是较小的数b,不开心的天数是a−b2.
#include <stdio.h>
int main(){int a,b,t;while(scanf("%d%d",&a,&b)2){if(a<b){ta;ab;bt;}printf("%d %d\n",b,(a-b)>>1);}
}
0034 - B - 判断三角…
LeetCode 面试题64. 求1+2+…+n
原题目:https://leetcode-cn.com/problems/qiu-12n-lcof/ 思路:
这个题不让用乘除,还不让用判断和循环,那么考虑递归和&&的短路特性。
&&的短路特性是指,a&&b,一旦a为false,则不…
泰勒公式(泰勒展开式)通俗介绍+本质详解
比较通俗地讲解一下泰勒公式是什么。 泰勒公式,也称泰勒展开式。是用一个函数在某点的信息,描述其附近取值的公式。如果函数足够平滑,在已知函数在某一点的各阶导数值的情况下,泰勒公式可以利用这些导数值来做系数,构建…
Gauss–Jacobi_quadrature(MATLAB)
function [t,w] = GaussJacobi(n,beta,alpha)
% [x,w] = GaussJacobi(n,alpha,beta)
% find Gauss-Jacobi nodes x(1)<
Definition of ‘blow up‘ in the context of PDEs
At one extreme, there are very dramatic examples of illposedness, such as blowup - various norms going to infinity in finite time - beyond which no reasonably strong notion of solution can be salvaged.
摘自Terence Tao的Nonlinear Dispersive Equations里3.8节…
推荐系统 理论笔记 二 (数学基础)
线性代数
微积分 梯度是一个向量,向量里的每一个值都是不同自变量(方向)的偏导数。 所以的偏导构成的向量,就是梯度。大小就是最快方向的变化值。
【复变函数】2021-9-14-复变函数/解析函数的一些想法(三)(算不上笔记)
一、区域:
邻域(圆形);去心邻域;无穷的邻域与去心邻域同样定义; 开集、连通集;边界; 区域,闭区域; 有界区域,无界区域; 概念定义不再…
数列极限:重要极限 π 与 e
数学分析笔记——总目录 文章目录数列极限:重要极限 π 与 e重要极限:π重要极限:e参考文献数列极限:重要极限 π 与 e
重要极限:π
圆周率,为圆周长与直径之比,记作 π\piπ 。
通常&#x…
数学分析:函数序列及其一致收敛性
文章目录函数序列及其一致收敛性函数序列函数序列的一致收敛性函数序列一致收敛性的判别法一致收敛的函数序列的性质参考文献函数序列及其一致收敛性 \quad此前,我们已经可以用收敛数列(或收敛的数项级数)来表示或定义一个数,接下…
Parseval–plancherel theorem
1、https://math.stackexchange.com/questions/669480/a-problem-about-laplace-transform-and-parseval-plancherel-theorem2、https://www.solveforum.com/forums/threads/a-problem-about-laplace-transform-and-parseval%E2%80%93plancherel-theorem.340747/3、https://han…
数学分析:换元积分法与分部积分法
8.2 换元积分法与分布积分法
一、换元积分法
定理 4:(第一类换元积分法) \quad设函数 f(x)f(x)f(x) 在区间 III 上有定义,φ(x)\varphi(x)φ(x) 在区间 JJJ 上可导,且 φ(J)⊂I\varphi(J) \subset Iφ(J)⊂I. 若不定…
【蓝桥杯集训1】前缀和专题(2 / 5)
目录
前缀和模板
!3956. 截断数组 - 前缀和枚举 前缀和模板
活动 - AcWing
import java.util.*;class Main
{static int N100010;static int[] anew int[N],snew int[N];public static void main(String[] args){Scanner scnew Scanner(System.in);int nsc.nex…
1600*C. Game On Leaves(博弈游戏树)
Problem - 1363C - Codeforces 解析: 我们将目标结点 x 当作树的根,显然,到当 x 的度为 1 的时候,此时行动的人胜利。 我们假设现在的情况为,只剩余三个点,再选择任意一个点,则对方获胜。但是两…
51nod 1677——treecnt
题意:给你n个结点,n-1条边,要从这n个结点里面选出k个结点,再选出最少边使这些结点之间相互连通,问对于所有选择k个结点的最小选择边数的总和是多少。
题解:因为每次选k个点其实是固定了的,所以…
11. 微积分 - 偏导数方向导数
文章目录 偏导数方向导数方向余弦投影继续讲方向导数Hi, 大家好。我是茶桁。 我们上节课学习了链式法则,本节课,我们要学习「偏导数」和「方向导数」。
偏导数
偏导数在导论课里面也提到过。偏导数针对多元函数去讲的。
多元函数是什么,我们拿个例子来看: 多元函数: y…
杭电ACM--2036,求任意多边形的面积(思维)
这道题中“每行的开始是一个整数n(3<n<100),它表示多边形的边数(当然也是顶点数),然后是按照逆时针顺序给出的n个顶点的坐标(x1, y1, x2, y2… xn, yn)”这么一句话是关键,下面所采用的公…
整除符号'|'(如 a|b)
数学符号“∣”的意义,如a∣b:
|为整除符号,对于整数a,b(a≠0),若存在整数k,使bka,则称a整除b,或b能被a整除,记为a∣b。
21. 概率与统计 - 数学期望、统计描述分布
文章目录 数学期望方差标准差协方差二项分布高斯分布中心极限定理泊松分布Hi, 你好。我是茶桁。
在上一节中,我们最后有谈到随机变量。在概率论几统计学中,描述一个随机变量的离散程度的有方差、标准差等等。那么在这节课中,我们就来好好看看这些概念。
不过在这之前呢,我…
一文通俗搞懂极限(一元/二元)、连续、无穷小比阶
极限作为考研数学的开篇,试图让我们接受"你可以无穷趋近,但你永远也不能达到"的状态,这种有悖常理的状态充满吊诡,加之一堆古希腊符号,让我们对"无穷"之下的不确定性感到畏惧。
不止是我们&#…
【概率】极大似然MLE 和最大后验 MAP,最大熵Maximum Entropy
mark
极大似然估计
最大后验估计
最大熵估计
参考资料
参数估计(2):极大似然,最大后验,贝叶斯推断以及最大熵
C#,史密斯数(Smith Number)的计算方法与源代码
一、关于史密斯数的传说 1、关于理海大学Lehigh University
理海大学(Lehigh University),位于宾夕法尼亚州(Pennsylvania)伯利恒(Bethlehem),由富有爱国情怀与民族精神的实业家艾萨…
数学回味系列之3 - 赛马问题
问题提出: 共有25匹马,有一个赛场,赛场有5个赛道,就是说最多同时可以有5匹马一起比赛。假设每匹马都跑的很稳定(可多次比赛),只通过马与马之间的比赛,没有计时器,试问&am…
AcWing算法提高课-5.6.2青蛙的约会
宣传一下 算法提高课整理
CSDN个人主页:更好的阅读体验 原题链接
题目描述
两只青蛙在网上相识了,它们聊得很开心,于是觉得很有必要见一面。
它们很高兴地发现它们住在同一条纬度线上,于是它们约定各自朝西跳,直到…
Noise Reduction Using a Median Filter(噪声去除的中值滤波方法)
摘 要:本实验主要实现图像的加噪和去噪。模拟数字图像的噪声主要由于噪声广泛存在于图像的产生和传输过程。图像传感器的工作情况受各种因素的影响,如图像的获取中的环境条件和传感器自身的质量。图像在传输过程中主要由于所用的传输信道的干扰而受到…
质因数,约数个数、约数和
质因数 质因数:一个数的约数为质数,则这个约数称为质因数 首先我们了解一下算数基本定理 算数基本定理:(欧几里得最早提出 Respect) 任何一个大于1的自然数 N,如果N不为质数,那么N可以唯一分解成有限个质数的乘积NP1^a1xP2 ^a2xP3 ^a3…Pn ^an,这里P1<…
质数检验(埃拉托色筛选法、根号x复杂度算法)
单次复杂度为O(根号x) 一个合数(非质数)x,一定可以分解为p*q,其中p小于等于根号x,q大于等于根号x 举例: 162x8,2<4,8>4 82x4,2<3倍根号二,4>3倍根号二 通过上述性质,可以不在遍历从2~x-1,而是可以从2 ~ 根号x,这样复杂度就变为O(根号x) 为什么呢? 因为只要找到一个…
差分数组(详解+例题)
差分数组 定义:所谓差分数组,就是将一个数组中后一项减去前一项形成新的数组 eg: 原数组 5 4 7 2 4 3 1 进行后一项减去前一项,第一项不变 5 、(4-5) 、(7-4)、(2-7)、(4-2)、(3-4)、(1-3) 差分数组:5 -1 3 -5 2 -1 -2 性质: 最主要的性质:差分数组求前缀和结果等于原数组 接着…
数学学学习之范数和距离的关系
1 范数 向量的范数可以简单形象的理解为向量的长度,或者向量到零点的距离,或者相应的两个点之间的距离。 向量的范数定义:向量的范数是一个函数||x||,满足非负性||x|| > 0,齐次性||cx|| |c| ||x|| ,三角不等式||xy…
Codeforces Round #342 (Div. 2)总结
A题:
A题题目链接
题目描述: A. Guest From the Pasttime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard outputKolya Gerasimov loves kefir very much. He lives in year 1984 and knows all the de…
常见数学公式和符号的英文读法大全
常见的数学公式和符号的英文读法,由于有些符号(比如求和符号、根号等)没法正常输入,所以直接上图了。方便有需要的朋友查阅。
4.2每日一题(求多元函数在某一点的微分)
1、分别求x和y的偏导,再相加即可
2、因为多元函数的表达式不方便求偏导,所以可以使用先代后求法: (1)对x偏导:把y0代入,很容易求出对x偏导的结果 (2)对y偏导:…
数值分析笔记——迭代法+代码实现
数值分析笔记——迭代法代码实现
问题:在可以使用直接法求出精确解的情况下,为什么还要使用迭代法求他的近似解呢?
因为我们求解的问题通常需要通过计算机设计算法来解决,当未知数非常多,问题规模非常大的时候&#…
java中与数学相关的类
1.Math 用于数学运算的各种方法公式,用的不多。其中的方法全部是静态的。 列举一些方法: 还有很多**static double random() 返回一个double值,大于或等于0.0小于1.0。区间【0,1); 2.BigDecimal float和double都不能完…
447. 回旋镖的数量
2021-09-13 LeetCode每日一题
链接:https://leetcode-cn.com/problems/number-of-boomerangs/
标签:数组、数学、哈希表 题目 给定平面上 n 对 互不相同 的点 points ,其中 points[i] [xi, yi] 。回旋镖 是由点 (i, j, k) 表示的元组 &…
①matlab的命令掌握
目录
输入命令
命名变量
保存和加载变量
使用内置的函数和常量 输入命令
1.您可以通过在命令行窗口中 MATLAB 提示符 (>>) 后输入命令
任务
使用命令 3*5 将数值 3 和 5 相乘。
答案
3*5 2.除非另有指定,否则 MATLAB 会将计算结果存储在一个名为 ans…
[Daimayuan] 数学(C++,最大公约数)
给定整数 n n n,胖教授想将 1 ∼ n 1∼n 1∼n这 n n n个数字分成两组,每一组至少有一个数,并且使得两组数字的和的最大公约数最大,请输出最大的最大公约数。
输入格式
一行一个整数 n n n。
输出格式
输出一行一个整数表示答…
数学分析:定积分的概念
数学分析笔记——总目录 文章目录定积分的概念定积分的产生背景定积分的定义参考文献定积分的概念
定积分的产生背景 \quad不定积分 与 定积分 是积分学中的两大基础问题,在不定积分部分,我们知道,不定积分是求导的逆运算,而本节…
线性基(插入与查询)
插入:
void ins(){
for(int i63;i>0;i--){if(x>>i&1){if(d[i])x^d[i];else{d[i]x;for(int j0;j<i;j)if(d[j]&&(d[i]>>j&1)){d[i]^d[j];}for(int ji1;j<64;j){if(d[j]>>i&1){d[j]^d[i];}cnt;break;}}}
}查询第k小
…
相对论-再看电动力学
前置 汇总表 前置 洛伦兹变换 前置 四维矢量及标积
动量四维矢量 标积 四维梯度定义:(这里的符号个人理解是人为定义的,为了纠正符号错误) 推导过程(对于一个标量函数,注意这里的符号有问题,因此定义四维梯度的时候要加个符号):
[牛客网Wannafly挑战赛23E]排序
###Description 随机一个2*n的排列,将奇数位从小到大排序,求逆序对个数的期望 比如说,4,6,1,5,3,2排序后会变成1,6,3,5,4,2,逆序对个数为8 n<5e7
###Solution 做了好几节数学课的说 根据期望的线性性,我们只需要枚…
2021ICPC网络赛Ⅱ(第二场)L Euler Function 线段树+欧拉函数定理
题目链接
题目大意
两种操作
0 l r w, for each index i∈[l,r], change xi to xiw.1 l r, calculate and print mod 998244353.其中\varphi (x_{i}) 就是区间内欧拉函数的和
题目思路
要做这个题首先要知道以下两个定理 我们先预处理出来一百以内的欧拉函数
以及一百…
0917-今天开始学习机器学习中的数学基础
[ ]1.学知识是为了应用的。学以致用,产生价值。 深度学习的梯度原来是来自方向导数。 贝叶斯公式其实我早就学过List item
汤姆·齐格弗里德《纳什均衡与博弈论》笔记(3)博弈论与生物学
第四章 史密斯的策略——进化、利他主义与合作 博弈论有助于解释在动物(包括人类)世界中社交行为的进化,解开了达尔文进化论中初始的谜团:为什么动物会合作?你可能会认为,斗争的生存法则将会助长自私。然而…
函数的连续性与间断点
连续性的概念及几何表达
我们用图像来对连续性进行表示: 函数连续性通俗的定义:当自变量x发生微小变化时,函数f(x)也发生微小变化,这就叫做函数的连续性。 函数连续的定义 当x趋近于x0时,f(x)接近于f(x0)
我们进行数…
【NOI2014模拟7.11】数学题(math)
Description
给出两个二维向量a和b,求两个整数λ1,λ2不同为0,使得λ1aλ2b最小。
Solution
富榄教我学数学w 为了方便我们约定|a|<|b|,a⋅b>0如果不是的话可以通过调整λ的正负性和交换a,b来完成。 我们要让|axby|最小 那么同时也就是让|ax…
f(x)是个什么玩意儿
从什么时候开始讨厌数学的呢,我也记不太清楚了。但是“函数”这两个字一直很令我不爽,尤其是“yf(x)”这个公式,我一直不明白这是个什么玩意儿,所以总搞不清楚一会儿yf(x),一会儿又特么xf(y),搞什么究竟是。…
Educational Codeforces Round 54 C. Meme Problem
题目意思:给你一个d,d满足abd和a*bd。如果有这样的a和b就输入Y和对应的a和b,不满足就输出N.误差不超过1e-6.
思路:这题看到ab和a*b想到的是维达定理。那么就有 x1x2-ba\frac{b}{a}ab x1 *x2ca\frac{c}{a}ac 原方程化简为x2x^2x2-ba\frac{b}{a}abx…
算法笔记(XI) 算法分析与勒贝格积分
放在前面的后记: 这篇小文简单记录了自己的一个小小发现,也就是勒贝格积分和算法分析方法上的一个等同点:其实现在我已经比以前更清楚的看到计算机科学与数学中的相贯通的地方,这也是我看了《算法导论》《具体数学》的部分内容后才…
简单理解非对称加密算法
最初理解非对称加密算法是一件很难的事,可能需要看一些晦涩难懂的读物看很长时间才能理解得了,所以今天我打算用一个简单的例子来解释非对称加密算法,希望可以帮助大家快速的理解这个概念。首先,我们设想这样一个场景:…
同构:编程中的数学(文末送书4本)
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…
多项式插值算法 python实现
算法思想:用多项式逼近原函数
import numpy as np
from numpy import *
import numpy.linalg as lg #numpy的线性代数函数库 linalg
import math
x[]
y[]
N10
pimath.pi
#形成十个(x,y)点
for i in range(N):x.append(round((-1(2/N)*(N-i)),3))
de…
有趣的微分方程传之可分离变量的微分方程
话说远古时期,有一大家族,家大业大,繁荣昌盛,但是好景不长,这个家族的x族和y族闹了矛盾,彼此分离。以前解决问题都是x,y族联合解决,现在只需要分开解决即可。由此,产生了可分离变量的…
Latex公式常见符号
Latex公式常见符号一、运算符号二、函数符号三、括号、箭头四、希腊字母资源下载地址:Latex公式常见符号.pdf
一、运算符号
序号数学符号Latex表达式助记1\times\timestimes2\div\divdiv3\pm\pmplus minus4∓\mp∓\mpminus plus5⋅\cdot⋅\cdotc dot6⋆\star⋆\starstart7ab\…
广州套刷公交卡数学建模
广州套刷公交卡数学建模前言一、问题描述二、数学建模三、问题求解总结前言
广州乘坐公交地铁优惠方案如下:每月前15次9.5折,第16次开始6折。公交通常是2元一次,地铁按里程分段收费,起步价格为2元。有的乘客单次乘坐地铁原价比较…
24. 图论 - 图的表示种类
Hi,你好。我是茶桁。
之前的一节课中,我们了解了图的来由和构成,简单的理解了一下图的一些相关概念。那么这节课,我们要了解一下图的表示,种类。相应的,我们中间需要穿插一些新的知识点用于更好的去理解图,比如说邻接矩阵。
图的表示
我们一般用什么样的形式来表示图…
【复变函数】2021-09-13-复变函数/解析函数的一些想法(一)(算不上笔记)
一:
复数的定义、共轭、运算; 复平面,模,辐角主值,三角坐标表示,指数表示; 复数乘积与商的r与θ,棣莫弗公式; 不再重复记录。 (纸质笔记已经记录)…
小学20以内加减法_自动生成器
package com;import java.awt.Color;
import java.awt.Font;
import java.awt.Graphics;
import java.util.ArrayList;
import java.util.List;
import javax.swing.JFrame;
import javax.swing.JPanel;public class Test4_36Arithmetics {//定义两个变量表示背景图的宽高stati…
Codeforces Round #539 (Div. 2)_C. Sasha and a Bit of Relax(异或)
题目链接:C. Sasha and a Bit of Relax
题目:
Sasha likes programming. Once, during a very long contest, Sasha decided that he was a bit tired and needed to relax. So he did. But since Sasha isnt an ordinary guy, he prefers to relax un…
数学分析:一元实函数论----一元实函数基础
数学分析:一元实函数论——一元实函数基础函数(一元实函数)基础函数(一元实函数)的概念函数(一元实函数)的表示方法解析法图形法表格法函数(一元实函数)的四则运算函数(一元实函数)的复合运算函数(一元实函数)的逆运算参考文献函数(一元实函数)基础
函数(一元实函数…
连续函数:闭区间上的连续函数
文章目录连续函数:闭区间上的连续函数有界性定理最值定理零点存在原理中间值定理参考文献连续函数:闭区间上的连续函数
有界性定理
最值定理
零点存在原理
中间值定理
参考文献
为数学而歌之伯努利家族
为数学而歌之伯努利家族 这是一个身负盛名的家族,从17世纪后半叶至20世纪30年代,伯努利家族的后裔至少有120位被人们追溯,他们涉及的领域有算术、几何学、天文学、数理音乐和文法、修辞、雄辩术。在这些领域都很有名望。最不可思议的是这个家…
连续函数:函数在区间上连续
文章目录连续函数:函数在区间上连续函数在开区间上连续函数在闭区间上连续参考文献连续函数:函数在区间上连续
函数在开区间上连续
函数在闭区间上连续
参考文献
牛顿-莱布尼茨公式练习习题
前置知识:牛顿-莱布尼茨公式
习题1
已知 F ( x ) ∫ 0 x 1 − t d t ( x ≤ 1 ) F(x)\int_0^x\sqrt{1-t}dt(x\leq 1) F(x)∫0x1−t dt(x≤1),求 F ′ ( x ) F(x) F′(x)
解: \qquad 当 x 0 ∈ [ 0 , 1 ] x_0\in[0,1] x0∈[0,1]时&…
第二类换元法三角代换专项训练
前置知识:第二类换元法
题1: 计算∫1(a2−x2)32dx\int \dfrac{1}{(a^2-x^2)^{\frac 32}}dx∫(a2−x2)231dx
解: \qquad令xasintxa\sin txasint,tarcsinxat\arcsin \dfrac xatarcsinax,dxacostdtdxa\cos …
codeforces 834C The Meaningless Game(数学题)
传送门:codeforces 834C题目大意:
两人进行比赛,初始分都为 1,每局选择一个自然数 k,胜者的得分乘以 k^2,败者的得分乘以 k,给出两人的最终得分,问这个得分是否有可能出现。思路&…
【概率论笔记】正态分布专题
文章目录一维正态分布多维正态分布n维正态分布二维正态分布一维正态分布
设X~N(μ,σ2)X\text{\large\textasciitilde}N(\mu,\sigma^2)X~N(μ,σ2),则XXX的概率密度为f(x)12πσe−(x−μ)22σ2f(x)\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}f(…
第二周周赛——加油 题解(分别出自HDU5615,HDU5586,codeforces 319B,codeforces 518C,codeforces 548D)
A题:
A题题目链接
题目描述: QAQ又遇到数学问题了 TimeLimit:1000MS MemoryLimit:65536KB64-bit integer IO format:%I64dProblem DescriptionJam有道数学题想向你请教一下,他刚刚学会因式分解比如说,x^26x5(x1)(x5)就好像形如 ax^2bxc &…
【第9题】容斥原理:P3197 [HNOI2008]越狱
题目:P3197 [HNOI2008]越狱
题目原文请移步下面的链接
https://www.luogu.com.cn/problem/P3197 参考题解:https://www.luogu.com.cn/problem/solution/P3197 标签:OI、 数学、容斥
题解
思路
第一点:排列组合的问题…
排列组合相关公式讲解(Anm,Cnm等)
两个性质: 1.C(n,m)C(n,n-m) 2.C(n,m)C(n-1,m)C(n-1,m-1);(编程时可用此递推)
LeetCode263. Ugly Number
文章目录 一、题目二、题解 一、题目
An ugly number is a positive integer whose prime factors are limited to 2, 3, and 5.
Given an integer n, return true if n is an ugly number.
Example 1:
Input: n 6 Output: true Explanation: 6 2 3 Example 2:
Input: …
备战蓝桥杯---数学基础3
本专题主要围绕同余来讲:
下面介绍一下基本概念与定理: 下面给出解这方程的一个例子: 下面是用代码实现扩展欧几里得算法:
#include<bits/stdc.h>
using namespace std;
int gcd(int a,int b,int &x,int &y){if(b…
分式理想 对偶群 对偶空间
参考文献:
Deitmar A. A first course in harmonic analysis[M]. 2005.Ideal quotient | encyclopedia article by TheFreeDictionaryFractional ideal | encyclopedia article by TheFreeDictionaryPontryagin duality | encyclopedia article by TheFreeDictiona…
数学回味系列之10 - 高楼扔鸡蛋
问题提出: 有座100层的建筑,鸡蛋从某一层扔下来有可能摔碎(可能是1楼,也可能是100楼)。 你手上有两个软硬程度一样的鸡蛋,要判断出来哪一层是鸡蛋可以安全落下的最高位置。 最少需要扔多少次?
…
【bzoj1257】[CQOI2007]余数之和sum
Description
给出正整数n和k,计算j(n, k)k mod 1 k mod 2 k mod 3 … k mod n的值,其中k mod i表示k除以i的余数。例如j(5, 3)3 mod 1 3 mod 2 3 mod 3 3 mod 4 3 mod 5010337
Input
输入仅一行,包含两个整数n, k。
Output
输出…
codeforces 1474 B Different Divisors
原题链接 题意
给你一个整数d让你找出最小的整数a a满足的条件是1.至少有4个因子,2.a的任意两个因子之差最少为d
思路 1.数论简单题,用到了线性筛求素数 2.我们观察样例,1肯定是选择的,最后一个因子肯定是a本身,然后…
求最大公约数和最小公倍数(四种)
辗转相除法
int measure(int x,int y)//x>y;
{int zy;while(x%y!0){zx%y;xy;yz;}return z;
}辗转相减法
int measure(int x,int y)
{while(x!y){if(x>y)x-y;elsey-x;}return x;
}穷举法
int measure(int x,int y)
{int z0;for(zmin(x,y);;x--){if(x%z0&&y%z0)…
Codeforces Round #326 (Div. 2)总结
A题:
A题题目链接
题目描述: A. Duff and Meattime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard outputDuff is addicted to meat! Malek wants to keep her happy for n days. In order to be happ…
2013年蓝桥杯试题解析(一)
1.猜年龄 美国数学家维纳(N.Wiener)智力早熟,11岁就上了大学。他曾在1935~1936年应邀来中国清华大学讲学。一次,他参加某个重要会议,年轻的脸孔引人注目。于是有人询问他的年龄,他回答说:“我年龄的立方是个4位数。我年…
Educational Codeforces Round 7总结
A题:
A题题目链接
题目描述: A. Infinite Sequencetime limit per test1 secondmemory limit per test256 megabytesinputstandard inputoutputstandard outputConsider the infinite sequence of integers: 1, 1, 2, 1, 2, 3, 1, 2, 3, 4, …
配置法 求解1D第二类线性的Fredholm积分方程 +MATLAB
function fen_f(x)
fx;
endfunction ffn(x)
fx/2-1/3;%MATLAB 将函数 传入另一个函数,比如这里的f是另一个函数传过来的,所以
%调用时,需要加
%如 tGauss_integral1(fn,0,1)等
%这是一个任意连续函数 都可以数值积分 的程序
function G Gaus…
Powers of i in Complex Numbers
1、https://math.stackexchange.com/questions/3168114/powers-of-i-in-complex-numbers?noredirect12、https://math.libretexts.org/Bookshelves/Precalculus/Book%3A_Trigonometry_(Sundstrom_and_Schlicker)/05%3A_Complex_Numbers_and_Polar_Coordinates/5.03%3A_DeMoivr…
【力扣周赛#334】6369. 左右元素和的差值 + 6368. 找出字符串的可整除数组 + 6367. 求出最多标记下标
目录
6369. 左右元素和的差值 - 前缀后缀和 ac
6368. 找出字符串的可整除数组 - 操作余数ac
6367. 求出最多标记下标 - 二分答案 贪心 6369. 左右元素和的差值 - 前缀后缀和 ac
class Solution {public int[] leftRigthDifference(int[] nums) {int nnums.length;int[] re…
拉格朗日中值定理习题
例1
设a>b>0a>b>0a>b>0,证明:a−ba<lnab<a−bb\dfrac{a-b}{a}<\ln\dfrac ab<\dfrac{a-b}{b}aa−b<lnba<ba−b
证: \qquad令f(x)lnxf(x)\ln xf(x)lnx,x∈(0,∞)x\in(0,\infty)x∈…
Android基础之J2se学习规划
这里不要看到j2se感觉是一个大方向就觉得有点难,想打退堂鼓了!那你就打错特错了!
如果你确实要深入学习的话确实要花许多功夫
但是知识基础的话就三个字
简单
简单
简单
额,这里好像只有两个字。
好了,不废话上…
3.16每日一题(区间在现求定积分)
解法一: 1、二倍角化简,为了使用公式把x消去,令t2x,跟换区间 2、因为三角函数的几何性质,即sinx在0到Π上时对称区间,所以可以只计算[ 0 , Π/2 ]上的面积,最后乘2即可。 注:换元后记…
1500*B. Zero Array(贪心数学找规律)
Problem - 1201B - Codeforces 解析: 因为每次减少2,如果总和为奇数肯定无法实现。 特例,如果某个数大于其他所有数的总和,同样无法实现。 其他均可实现。
#include<bits/stdc.h>
using namespace std;
#define int long l…
剑指 Offer(第2版)面试题 62:圆圈中最后剩下的数字
剑指 Offer(第2版)面试题 62:圆圈中最后剩下的数字 剑指 Offer(第2版)面试题 62:圆圈中最后剩下的数字解法1:环形链表解法2:数学 剑指 Offer(第2版)面试题 62…
勘察设计考试公共基础之数学篇
1、数学
向量点积:向量叉积:平面的法向量为n(A,B,C),则该平面的点法式方程为:
A(x-x0)B(y-y0)C(z-z0)0
两平…
多平面包络的圆柱体参数估计
多平面包络的圆柱体参数估计
场景
现有多个空间平面包络一个柱体,从圆柱顶端俯视如图所示: 中心位置为圆柱实际所在位置。现在已知这些平面的参数(每个平面的方程均为axbyczd0形式, 参数为a,b,c,d),希望求解它们包络…
如何判断n(n-1)/2的奇偶性【数学问题】
这道题是我复习线性代数时遇到,个人觉得很有意思,所以拿出来分享一下思路。 首先,不管n是奇数还是偶数,那么n-1的奇偶性肯定与n相反,那么对于n(n-1)/2来说,也就是一个奇数乘以(偶数除以2&#x…
关于数据结构,算法,和数学的想法,认知,和计划
技术发展的太快了,心里感觉总有压力,感觉有学不完的东西,不会的东西太多,又不能成为超人,所以现实点,要抓住主线,抓住重点。
首先我认为数据结构,算法,和数学是计算机世…
【面试经典150 | 数学】Pow(x, n)
文章目录 写在前面Tag题目来源题目解读解题思路方法一:快速幂-递归方法二:快速幂-迭代 其他语言python3 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主…
(邱维声)高等代数课程笔记:矩阵的加法、数量乘法与乘法
(邱维声)高等代数课程笔记:矩阵的加法,数量乘法与乘法 \quad前面已经看到,矩阵的初等行变换、矩阵的秩 在线性方程组理论中起着非常重要的作用,因此,系统地研究一下矩阵是非常有必要的。 \quad本…
定积分解题的一些特殊方法习题
前置知识:定积分解题的一些特殊方法
习题1
比较定积分的大小: ∫ 0 1 1 1 x 2 d x ‾ ∫ 0 1 1 1 x 4 d x \int_0^1\dfrac{1}{1x^2}dx\underline{\qquad}\int_0^1\dfrac{1}{1x^4}dx ∫011x21dx∫011x41dx
解: \qquad 因为在 …
LaTex数学公式中常用的符号及标记
LaTex数学公式中常用的符号及标记 最近使用typora记录笔记时,经常需要打印数学公式,因此在网上找了一篇符号表比较齐全的文章:LaTeX数学公式的符号表示。这里我只列出其中一小部分。 另外提一下LaTex行内公式和行间公式的编写格式:…
定积分的下限能否大于上限
前置知识:黎曼积分的概念
定积分的下限能否大于上限
在积分的定义中,都是假设 a < b a<b a<b。但有时候,定积分的下限可以大于上限。若 a ≥ b a\geq b a≥b,那定积分的值如下 ∫ a b f ( x ) d x − ∫ b a f ( x ) …
3.5每日一题(求齐次方程组的特解)
1、判断类型选择方法:看出为齐次方程(次幂都一样)
2、 化为变量可分离;按变量可分离的方法求出通解(此题等式两边同时除以 x )
3、把x1,y0带入通解,定常数C,求出特解
…
数列极限:数列极限的性质
数学分析笔记——总目录 文章目录收敛数列的性质数列极限的唯一性收敛数列的有界性数列极限的保序性数列极限的夹逼性数列极限的运算性质——四则运算数列极限的和、差运算数列极限的乘运算数列极限的商运算参考文献收敛数列的性质 \quad这一节,介绍收敛数列的一些性…
数学分析:集合理论----习题
集合理论:习题 1.\mathbf{1.}1. 证明由 nnn 个元素组成的集合 T{a1,a2,⋯,an}T\{a_1,a_2,\cdots,a_n\}T{a1,a2,⋯,an} 有 2n2^{n}2n 个子集。 证明:
从集合 TTT 中任取 k(k0,1,2,⋯,n)k(k0,1,2,\cdots,n)k(k0,1,2,⋯,n) 个元素组成集合࿰…
数列极限:无穷量与待定型
数学分析笔记——总目录 文章目录数列极限:无穷量与待定型无穷量无穷小量无穷大量正无穷大量负无穷大量定号无穷大量无穷小量与无穷大量的关系待定型00\frac{0}{0}00 型Stolz 定理参考文献数列极限:无穷量与待定型
无穷量
无穷小量
定义(…
2023蓝桥杯大学A组C++国赛游记+个人题解
Day0
发烧了一晚上没睡着,感觉鼻子被打火机烧烤一样难受,心情烦躁
早上6点起来吃了个早饭,思考能力完全丧失了,开始看此花亭奇谭
看了六集,准备复习数据结构考试,然后秒睡
一睁眼就是下午2点了
挂了个…
数学分析:集合的基本概念
文章目录数学分析:集合的基本概念集合基础:定义集合基础:表示法枚举法枚举法——有限集合枚举法——无限集合描述法集合基础:性质集合基础:关系蕴含子集真子集相等参考文献数学分析:集合的基本概念
集合基…
存在隐函数的变限积分求导习题
前置知识:存在隐函数的变限积分求导
习题
设函数 y y ( x ) yy(x) yy(x)由方程 ∫ 0 y e t 2 d t ∫ 0 sin x cos 2 t d t 0 \int_0^ye^{t^2}dt\int_0^{\sin x}\cos^2tdt0 ∫0yet2dt∫0sinxcos2tdt0,求 d y d x \dfrac{dy}{dx} dxdy
解…
刷题记录:牛客NC13611树
传送门:牛客
题目描述:
shy有一颗树,树有n个结点。有k种不同颜色的染料给树染色。一个染色方案是合法的,当且仅当对于所
有相同颜色的点对(x,y),x到y的路径上的所有点的颜色都要与x和y相同。请统计方案数。
输入:
4 3
1 2
2 3
2 4
输出:
39…
GDI+下字体大小自适应方案初探
在某个瞬间,我忽然发觉,三体或是AI,本质上是非常相近的事物,甚至在面对任何未知领域的时候,人类总会不自觉地划分为降临派、拯救派和幸存派。姑且不论马斯克等人叫停 GPT-5 的真实动机如何,当大语言模型(LL…
[Daimayuan] 三回文序列(C++,前缀和)
给定一个长度为nnn的序列aaa。
我们定义三回文序列是形如a...a⏟k1b...b⏟k2a...a⏟k1\underbrace{a...a}_{k_1}\underbrace{b...b}_{k_2}\underbrace{a...a}_{k_1}k1a...ak2b...bk1a...a的序列,例如:[1,1,1,2,2,1,1,1][1,1,1,2,2,1,1,1][1,1,1,…
POJ - 2282 The Counting Problem(数位DP 计数问题)
题目如下:
Given two integers a and b, we write the numbers between a and b, inclusive, in a list. Your task is to calculate the number of occurrences of each digit. For example, if a1024a 1024a1024 and b1032b 1032b1032, the list will be 10241…
算法工程师大致是做什么的
作者: 龙心尘 时间:2021年1月 出处:https://blog.csdn.net/longxinchen_ml/article/details/113074403
其实这是一个不太好解释的问题,因为并没有一个完备的定义。笔者在算法领域遇到了不少同行,发现各自的工作侧重点…
关于补码的深入探讨(未完待续)
负数
负数可以认为是当前数量相对基准值的偏移:比如说0下3度,可以表示为“-3度”负数有时隐藏在被动语境里面:比如说一个箱子可以装16瓶水,装了11瓶,我们可以说装了11瓶,也可以说差5瓶就装满一个箱子了负数…
【原创】二阶常系数非齐次线性微分方程求特解
二阶常系数非齐次线性微分方程求特解 (一)求特解时的题目问法 (1)求微方满足已给初值条件的特解 (2)设函数yy(x)满足微方***,y(x1)a,y(x2)b,求y(x) [相当于确定一个函数&…
承诺协议:定义 构造
文章目录 安全性定义方案构造基于 OWP 存在性基于 DL 假设基于 OWF 存在性基于 DDH 假设 总结 安全性定义
承诺协议(Commitment Scheme)是一个两阶段的两方协议。一方是承诺者(Committer) C C C,另一方是接收者&#…
【高数+复变函数】傅里叶积分
文章目录 【高数复变函数】傅里叶积分2. 傅里叶积分2.1 复数形式积分公式2.2 三角形式 上一节:
【高数复变函数】傅里叶级数 【高数复变函数】傅里叶积分
2. 傅里叶积分
在上一节中,我们知道了傅里叶级数的基本知识,其中,周期为…
积分第一中值定理习题
前置知识:积分第一中值定理
习题1
求证: lim n → ∞ ∫ 0 π 2 sin n x d x 0 \lim\limits_{n\to \infty}\int_0^{\frac{\pi}{2}}\sin^nxdx0 n→∞lim∫02πsinnxdx0
证明: \qquad 令 δ → 0 \delta\to 0^ δ→0&#x…
LeetCode 1281. 整数的各位积和之差
原题目:https://leetcode-cn.com/problems/subtract-the-product-and-sum-of-digits-of-an-integer/ 代码:
class Solution {
public:int subtractProductAndSum(int n) {int sum0,pro1;while(n>0){sum n%10;pro * n%10;n / 10;}return pro-sum;}
}…
【概率论】关于为什么样本标准偏差分母是n-1的进一步理解
上接物理实验引发的思考:总体标准偏差和样本标准偏差的区别是什么?标准偏差和标准误的区别是什么?,现在系统地学了概率论与数理统计,有了新的理解。 首先我们再回顾一些概念。设总体为XXX,样本为X1,X2,⋯,X…
【概率论】期末复习笔记:数理统计学的基本概念
数理统计学的基本概念目录一、总体与样本二、样本数据的整理1. 样本频数分布与频率分布2. 频率直方图3. 经验分布函数三、统计量1. 统计量的概念2. 几个常用的统计量1) 样本均值2) 样本方差和样本标准差3) 样本矩4) 顺序统计量5) 样本极差6) 样本ppp分位数四、抽样分布1. Γ\Ga…
【数学思维】数理经济中一些基本概念
【数学思维】数理经济中一些基本概念开集 open set 与闭集 closed set紧集 compact set集合有界 bounded set度量空间 metric space欧式空间 euclidean space闭包 closure上包络 upper envelope、下包络 lower envelope上极限 limit superior、下极限 limit inferior左连续、右…
线段树(原理,模板)
文章目录线段树线段树代码(单点修改、区间查询)懒惰标记与区间修改树状数组与区间修改线段树
线段树是用来维护 区间信息 的数据结构
它可以在 O(logn)O(\log n)O(logn) 的时间复杂度内实现单点修改、区间修改、区间查询(区间求和,求区间最大值&…
【Maki ‘ s Lab学习讲座】超前学习法
作者:MakiMaki的完美算术教室 排版: PenguinIT鹅 当人们愉快地承受苦难时,苦难也会变得美丽,这不是麻木,而是由于心灵的伟大。 ——亚里士多德
Maki’s Lab简介:
Maki’s Lab核心成员来自多伦多大学,清华大学等世界各地名校。M…
超越象限:解密 α 碎片的归属问题
文章目录 参考环境α 碎片的归属问题问题概述终边相同角圆心角终边相同角 象限角 描述象限角第一象限角任意象限角 特殊方案问解 叠加坐标系上部下部叠加坐标系 一般方案问解任意角 α分析绘图要领叠加坐标系N-N 参考
项目描述搜索引擎Google 、Bing百度百科首页佟大大还是ETT…
【复变函数笔记】洛朗级数、留数及其应用
文章目录 一、复变函数项级数泰勒级数洛朗级数 二、解析函数的孤立奇点三、留数与留数定理四、留数在计算实积分中的应用1. 形如 ∫ 0 2 π R ( cos θ , sin θ ) d θ \int_0^{2\pi}R(\cos\theta,\sin\theta)\mathrm{d}\theta ∫02πR(cosθ,sinθ)dθ的积分2. 形如 …
用斐波那契分解正整数
https://vjudge.net/contest/591700#problem/C 观察这个形式,如果交替做,就是个斐波那契数列
打表可得,任何正整数都可以大约由 log \log log 个斐波那契数加起来
然后直接拼斐波那契数即可
#include<bits/stdc.h>
using namesp…
MATLAB | πDay快乐,pi居然有这么多炫酷好玩的可视化
πDay快乐!
3.14 π Day 到了,本期给出一些非常炫酷的pi的可化并给出完整 MATLAB 代码。 首先,我们要获得pi的前n位小数,需要编写如下代码(为了防止不精准会多取几位尾数,用的时候再进行一次取前多少位的操作):
func…
【机器学习算法复现】逻辑回归解决分类问题,从数学原理走一遍流程。复习一下一些可视化展示的应用
逻辑回归 Logistic Regression 虽然被称为回归,但其实际上是分类模型,并常用于二分类。Logistic Regression 因其简单、可并行化、可解释强深受工业界喜爱。Logistic 回归的本质是:假设数据服从这个分布,然后使用极大似然估计做参…
傅里叶分析之掐死教程(完整版)
原文见:https://zhuanlan.zhihu.com/wille/19763358作 者:韩 昊 知 乎:Heinrich 微 博:花生油工人 知乎专栏:与时间无关的故事 谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张…
用梯度下降的方式来拟合曲线
文章目录1. 简述2. 理论原理以二次函数为例整体的梯度下降步骤:3. 编码实现初始化权重矩阵计算损失和梯度更新权重4. 结果首先对上一篇文章中的真实数据拟合。测试拟合高次曲线方程数据是2阶的,拟合方程是2阶的数据是4阶的,拟合方程也是4阶的…
Branching Program(5-PBP)
参考文献:
Lee C Y. Representation of switching circuits by binary-decision programs[J]. The Bell System Technical Journal, 1959, 38(4): 985-999.Masek W J. A fast algorithm for the string editing problem and decision graph complexity[D]. Massach…
原生js开发简易语音发声的计算器
前言:由于数学比较烂,只懂导数与微分,也正在研究半球几何,对于涉及到RMB的计算总怕算错几个小数点,于是使用简易的js开发计算器,这里并没有高精度的计算,还需优化。也没有运用到高大上的jquery。…
快速傅里叶变换Java版本
随手翻起大学时代自己手写的代码,代码写的不是很好,请参考。不喜勿喷。只能进行整的快速傅里叶变换
import java.util.*;
import java.lang.Math;
public class fastft
{public static void main(String[] args){double[] c{2,3,4,5,6,7,8,9};fft ftnew…
java中Math常用的数学函数
最近AI比较火,于是没事自己看下深度学习等方面的文章。 深度学习中的各种算法,用到了数学领域的很多公式、函数,回头想要敲代码熟悉一下这些算法时,发现很多公式、函数不用用代码写了,还要翻Math类。所以在这里记录一…
LeetCode 204. 计数质数
原题目:https://leetcode-cn.com/problems/count-primes/ 代码1;
class Solution {private:bool find(int a){for(int i2;i*i<a;i){if(a%i0) return false;}return true;}
public:int countPrimes(int n) {int count 0;for(int i2;i<n;i){if(find(i)) count…
LeetCode 1073. 负二进制数相加:简单算法 + 原理解析
【LetMeFly】1073.负二进制数相加
力扣题目链接:https://leetcode.cn/problems/adding-two-negabinary-numbers/
给出基数为 -2 的两个数 arr1 和 arr2,返回两数相加的结果。
数字以 数组形式 给出:数组由若干 0 和 1 组成,按最…
不定积分题型简单总结
不定积分 考研数学复习笔记,用来复习知识点用,如有不足还请指出,Thanks♪(・ω・)ノ 文章目录 不定积分1 原函数/不定积分 概念和性质2 原函数存在定理3 不定积分的基本公式4 不定积分的基本计算4.1 三角代换型…
无穷带来的直觉不靠谱
一、背景
话不多说直接上道具;错了…直接上问题。 请用直觉和数学逻辑告诉我下面三个问题的答案?
S11-11-11-11-1… 问:S1等于多少?
S21-23-45-67… 问:S2等于多少?
S31234567… 问:S3等于多…
LeetCode 1323. Maximum 69 Number
原题目:https://leetcode-cn.com/problems/maximum-69-number/ 思路:
使用到了to_string 和stoi两个函数 代码;
class Solution {
public:int maximum69Number (int num) {string s to_string(num);for(int i0;i<s.size();i){if(s[i] 6){s[i] 9;b…
LeetCode-878. 第 N 个神奇数字【数学,二分查找,找规律】
LeetCode-878. 第 N 个神奇数字【数学,二分查找,找规律】 题目描述:解题思路一:二分答案容斥原理。给定一个上下界,然后依次增大下界或者减小上界,直到只剩一个答案。容斥原理是,加上两个集合&a…
数学回味系列之24 - 黑白子交换
问题提出: 有三个白子和三个黑子如下图布置: ○ ○ ○ . ● ● ● 用最少的步数将上图中白子和黑子的位置进行交换: ● ● ● . ○ ○ ○ 游戏规则: (1) 一次只能移动一个棋子; (2) 棋子可以向空格中移动࿰…
数学回味系列之23 - 小明买书
问题提出: 小明假期同爸爸一起去书店,他选中了六本书,每本书的单价分别为:3.1,1.7,2,5.3,0.9和7.2。不巧的是,小明的爸爸只带了十几块钱,为了让小明过一个愉快…
【计算几何】判断多边形边界顺逆时针 C++代码实现
文章目录 一、多边形边界顺序二、数学原理2.1 Green公式2.2 鞋带公式 三、代码实现 一、多边形边界顺序
多边形可以由一个点集 { v 1 , v 2 , . . . , v n } \{v_1,v_2,...,v_n\} {v1,v2,...,vn} 表示,构成多边形的点集确定,多边形边界的顺序也就…
数学回味系列之19 - 有趣的数字
发现一些比较有意思的数,大家一起来认识一下: 分别是 阿姆斯特朗数、完全数、自守数、回文数 。 阿姆斯特朗数: 如果一个正整数等于其各个数字的立方和,则称为 阿姆斯特朗数 (也称自恋性数)。 比如 153 1^3 5^3 3^3 ÿ…
数学回味系列之18 - 哥德巴赫猜想
问题提出: 哥德巴赫猜想是世界近代三大数学难题之一。 哥德巴赫是德国一位中学教师,也是一位著名的数学家,生于1690年,1725年当选为俄国彼得堡科学院院士。 1742年,哥德巴赫在教学中发现,任意一个大于6的偶…
数学回味系列之17 - 三色球问题
问题提出: 口袋里有12个球,其中有3个红的,3个白的 和 6个黒的,问从中任取8个共有多少种不同的颜色搭配? 解题思路: 设任取的红球个数为 i,白球个数为 j,则黒球个数为 8-i-j…
数学回味系列之16 - 爱因斯坦台阶问题
问题提出: 爱因斯坦曾经提出过这样一道有趣的数学题:有一个长阶梯,若每步上2阶,最后剩下1阶;若每步上3阶,最后剩2阶;若每步上5阶,最后剩下4阶;若每步上6阶,最…
数学回味系列之8 - 绳子计时问题
问题提出: 烧一根不均匀的绳,从头烧到尾总共需要 1个小时。现在有若干条材质相同的绳子,问如何用烧绳的方法来计时 四十五分钟 呢?
解题思路: 这里的关键点在于:绳子可以两头同时点燃。 推断:…
Lucas定理和拓展Lucas定理
用途
对于一个组合数求值的问题,一般运用阶乘来求,但有时候阶乘太大,就会超时。
而 LucasLucasLucas 定理和拓展 LucasLucasLucas 定理就是用来解决在模意义下求值的问题。(但有个前提,就是你的模数必须比较小&#…
数学回味系列之5 - 三人分蛋糕问题
问题提出: 三个人分一块蛋糕,如何让每个人都觉得公平? 解题思路:
● 最公平的方案 - 先分后选 由 A 将蛋糕分成3块,BC选择其中两块; B重新对 选择的两块二次分割,C先选,剩下的一块…
Fractional Laplacian
1、https://mathoverflow.net/questions/295337/integral-of-fractional-laplacian-is-zero2、https://bibleandbookcenter.com/read/the-fractional-laplacian/3、https://web.ma.utexas.edu/mediawiki/index.php/Fractional_Laplacian
sin x和cos x的若干次方的定积分
sin x和cos x的若干次方的定积分 ∫ 0 π 2 sin n x ∫ 0 π 2 cos n x { n − 1 n n − 3 n − 2 ⋯ 1 2 π 2 n 为偶数 n − 1 n n − 3 n − 2 ⋯ 1 2 1 n 为奇数 \int_0^{\frac{\pi}{2}}\sin^nx\int_0^{\frac{\pi}{2}}\cos^nx \begin{cases} \dfrac{n-1}{n…
定积分的计算(分段积分)习题
前置知识:定积分的计算(分段积分)
习题1
计算 ∫ 1 e e ∣ ln x ∣ d x \int_{\frac 1e}^e|\ln x|dx ∫e1e∣lnx∣dx
解: \qquad 原式 ∫ 1 e 1 − ln x d x ∫ 1 e ln x d x − ln x ∣ 1 e 1 ln x ∣…
《离散数学》:集合、关系和函数
〇、前言
这章将会对集合、以及集合之上的关系、以及两个集合之间的映射情况做一个细致的讨论。集合作为数学和其他领域中的基础概念,具有广泛的应用和重要的地位。它为数学建立了基本的体系和推理方法,为各个领域的研究和应用提供了一种统一的描述和分…
2019牛客暑期多校训练营(第十场)D(扩展中国剩余定理+大整数防爆)
用中国剩余定理要求各个数直接互质,而扩展中国剩余定理则没有这个要求。 扩展中国剩余定理裸题,板子记好了。 因为数很大,过程可能会爆,所以可以用python,或者__int128. 代码如下:
#include<iostream&g…
【算法】数学相关知识总结
文章目录 gcd 和 lcm取模运算 %求一个点和一片矩形区域之间的最短距离 本文用于记录一些关于算法题中偶尔被使用到的数学相关知识。
gcd 和 lcm
gcd 和 lcm 分别是 最大公约数(Greatest common divisor) 和 最小公因数(Least Common Multip…
【YBT2023寒假Day13 B】马可波罗(博弈论)(数学)
马可波罗
题目链接:YBT2023寒假Day13 B
题目大意
有 n 堆石子,每对有 ai 个,两个人轮流取,每次可以选一堆石子,取至少 1 个至多 x 个石子。 无法操作着输。 然后问你当 x 分别是 1~n 时,是先手必胜还是后…
离散数学中deg()是什么
设无向图 G (V,E),顶点v(v ∈ V)关联的边数称作该顶点的度数,记为deg(v)
deg(v) 0,则v称为孤立点 deg(v) …
信号与系统复习笔记——采样
信号与系统复习笔记——采样与通讯系统
采样定理
冲激串采样函数可表示为: p ( t ) ∑ n − ∞ ∞ δ ( t − n T ) p(t) \sum_{n-\infty}^{\infty} \delta(t - nT) p(t)n−∞∑∞δ(t−nT)
周期 T T T 称为采样周期,而 ω s 1 T \omega_s …
命题逻辑的基本概念-习题
1.1判断下列句子是否为命题
(1)444 是素数。 是命题,且为假命题。 (2)5\sqrt 55 是无理数 是命题,且为真命题。 (3)xxx 大于 yyy,其中 xxx 和 yyy 是任意的两…
存在隐函数的变限积分求导
前置知识
隐函数求导变限积分求导 介绍
在前置知识中,我们已经知道隐函数和变限积分是什么了。那把这两样东西放在一起,会怎么样呢?
这类题目可能看起来很吓人,其实只要将变限积分看作一个函数,然后就可以用隐函数求…
力扣每日一题:810. 黑板异或游戏
目录题目:810. 黑板异或游戏示例提示:解题思路解题代码题目:810. 黑板异或游戏
难度: 困难
题目: 黑板上写着一个非负整数数组 nums[i] 。Alice 和 Bob 轮流从黑板上擦掉一个数字,Alice 先手。如果擦除一…
常用数学知识整理——C/C++代码实现
目录一、平年 or 闰年二、最大公约数2.1 辗转相除法三、最小公倍数3.1 穷举法3.2 公式法四、质数 or 合数4.1 判断是否为质数4.2 找到质数序列五、奇数 or 偶数5.1 求余法5.2 位与法写在前头:因为不管生活中或者编程或者是在写数学题的时候,经常遇到一些…
数学相关 - HyperLogLog算法原理
应用场景
当需要对大量数据做去重计数, 例如统计一个页面的UV(Unique Visitor, 独立访客), 或者用户搜索的关键词数量, 比较容易想到的方案有
存储到数据库表, 使用distinct count计算使用Redis的set, bitmap等数据结构
但都存在一些问题, 随着数据量增加, 存储空间占用越来…
数学之美中的马尔科夫链
与HMM模型相关的“有用”的问题是评估(前向算法)和解码(维特比算法)——它们一个被用来测量一个模型的相对适用性,另一个被用来推测模型隐藏的部分在做什么(“到底发生了”什么)。可以看出它们都…
两个不相交的闭集并不能保证两个集合可分
首先, 我们重申以下闭集的定义。如果一个集合的聚点都属于这个集合本身吗,那么这个集合是一个闭集。
比如[0,1][0,1][0,1]就是一个闭集,而(0,1](0,1](0,1]就不是。
接下来, 我们再来定义两个集合是否可分。首先我们要明确的一点…
定积分求平面区域的面积习题
前置知识:定积分求平面区域的面积
习题
设平面区域由曲线 y x 2 − 1 yx^2-1 yx2−1和 y − x 2 1 y-x^21 y−x21围成,求 D D D的面积 S S S
解: \qquad 两曲线的交点为点 ( − 1 , 0 ) (-1,0) (−1,0)和点 ( 1 , 0 ) (1,0) (1,0)&…
定积分求平面区域的面积
前置知识:黎曼积分的概念
介绍
由前置知识可得,黎曼积分可以求 x a xa xa, x b xb xb, x x x轴和 y f ( x ) yf(x) yf(x)围成的图形, S ∫ a b f ( x ) d x S\int_a^bf(x)dx S∫abf(x)dx
那么,我们…
【工科数学分析】2021-10-07-工科数学分析叒复习(三)
【前几天知道了一些好玩的事情,刘徽不是按照割圆法求出的圆周率,是后人猜测他用割圆法做出的圆周率】 【计算机体系结构的七层抽象给我留下的印象异常的深刻,让我不禁开始思考一个问题:多层级的抽象里有多少可挖掘的东西ÿ…
【周赛】第一周周赛——欢迎16级的新同学题解(题目出自codeforces 318A,546A,431C,665E,HDU 4104)
A题:
A题题目链接
A题题目描述: Home W的数学 TimeLimit:1000MS MemoryLimit:256MB64-bit integer IO format:%I64dProblem Description我们都知道,Home W的数学最厉害了。有一天,他又开始开动脑筋了,他想…
C语言中 ln(以自然对数e为底) lg(以十为底) 以及logab(以a为底,b为真数)的相关知识
总所周知,我们在高中学过对数函数,记作ylogax。下面是百度百科关于对数函数的描述: 对数的定义:一般地,如果axN(a>0,且a≠1),那么数x叫做以a为底N的对数,记…
CF1528F AmShZ Farm 题解
CF1528F 其实不难,但是又有懂得都懂的感觉。 某谷的翻译真的鬼畜。 题目大意:
一个合法的序列 AAA 是 ∀j≤n,∑i1n[ai≥j]≤n−j1\forall j \le n, \sum_{i 1} ^ n [a_i \ge j] \le n - j 1∀j≤n,∑i1n[ai≥j]≤n−j1。
给了一个限制 BBB 序列…
CF1383C 题解
CF1383C
观察一下题目的性质,他说了同一种颜色可以有若干个一起变色,那么我们考虑将同一种颜色看成相同的东西。
考虑对于其建图,也就是如果 AiA_iAi 变成 BiB_iBi 就建立 Ai→BiA_i \to B_iAi→Bi 的边。
然后本质上就是叫我们重…
数学分析:数项级数的概念
数项级数的概念
一、引言
在正式进行数项级数的学习之前,先考虑这样一个问题:
公元前 450450450 年,古希腊有一位著名的学者芝诺(Zeno)曾提出了若干个影响数学史发展的悖论。考虑其中一个非常著名的悖论:…
数学分析:函数的可积条件
文章目录函数的可积条件函数可积的必要条件函数可积的充要条件参考文献函数的可积条件
函数可积的必要条件 \quad在给出函数可积的充要条件之前,先来看函数可积的一个必要条件。
定理 1(可积的必要条件):若函数 f(x)f(x)f(x) 在…
数学分析:L‘Hospital 法则
数学分析笔记——总目录 文章目录LHospital 法则函数极限中的待定型处理 00\frac{0}{0}00 型的 LHospital 法则处理 ∗∞\frac{*}{\infty}∞∗ 型的LHospital 法则参考文献L’Hospital 法则
函数极限中的待定型 \quad接下来,我们只讨论如何使用 L’Hospital 法…
数学分析:Taylor多项式
数学分析笔记——总目录 文章目录Taylor 公式多项式函数的 Taylor 公式任意函数的Taylor公式带 Peano 余项的 Taylor 公式带Lagrange 余项的 Taylor 公式Maclaurin 公式参考文献Taylor 公式
多项式函数的 Taylor 公式 \quad设 p(x)p(x)p(x) 是 nnn 次整多项式: p(x…
51Nod 1009 数字1的数量 (数学
1009 数字1的数量基准时间限制:1 秒 空间限制:131072 KB 分值: 5 难度:1级算法题 收藏 关注 给定一个十进制正整数N,写下从1开始,到N的所有正数,计算出其中出现所有1的个数。 例如:n 12&am…
牛客寒假算法基础集训营6_A出题(数学)
题目链接:https://ac.nowcoder.com/acm/contest/332/A
题目描述
小B准备出模拟赛。 她把题目按难度分为四等,分值分别为6,7,8,9。 已知小B共出了m道题,共n分。 求小B最少出了多少道6分题。
解题思路: 显然,有解…
海伦公式(求三角形面积)
已知三角形的三条边长a,b,c,求面积s:
海伦公式: 其中: double p(abc)/2.0;
double ssqrt(p*(p-a)*(p-b)*(p-c));
2020年高教社建模国赛真题A题--炉温曲线
2020年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”) A题 炉温曲线
在集成电路板等电子产品生产中,需要将安装有各种电子元件的印刷电路板放置在回焊炉中,通过加热,将电子…
2020年高教社建模国赛真题B题--穿越沙漠
2020年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”) B题 穿越沙漠 考虑如下的小游戏:玩家凭借一张地图,利用初始资金购买一定数量的水和食物(包括食品和其他日常用品&…
2020年高教社建模国赛真题C题--中小微企业的信贷决策
2020年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”) C题 中小微企业的信贷决策 在实际中,由于中小微企业规模相对较小,也缺少抵押资产,因此银行通常是依据信贷政策、企业的…
2020年高教社建模国赛真题E题--校园供水系统智能管理
2020年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”) E题 校园供水系统智能管理 校园供水系统是校园公用设施的重要组成部分,学校为了保障校园供水系统的正常运行需要投入大量的人力、物力和财力…
2020年高教社建模国赛D题--接触式轮廓仪的自动标注
2020年高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”) D题 接触式轮廓仪的自动标注
轮廓仪是一种两坐标测量仪器(见图1),它由工作平台、夹具、被测工件、探针、传感器和伺…
470. 用 Rand7() 实现 Rand10()
2021-09-05 LeetCode每日一题
链接:https://leetcode-cn.com/problems/implement-rand10-using-rand7/
标签:数学、拒绝采样、概率与统计、随机化 题目 已有方法 rand7 可生成 1 到 7 范围内的均匀随机整数,试写一个方法 rand10 生成 1 到 …
789. 逃脱阻碍者
2021-08-22 LeetCode每日一题
链接:https://leetcode-cn.com/problems/escape-the-ghosts/
标签:数组、数学 题目 你在进行一个简化版的吃豆人游戏。你从 [0, 0] 点开始出发,你的目的地是 target [xtarget, ytarget] 。地图上有一些阻碍者…
1137. 第 N 个泰波那契数
2021-08-08 LeetCode每日一题
链接:https://leetcode-cn.com/problems/n-th-tribonacci-number/
标签:数学、记忆化搜索、动态规划 题目 泰波那契序列 Tn 定义如下:
T0 0, T1 1, T2 1, 且在 n > 0 的条件下 Tn3 Tn Tn1 Tn2
给你…
810. 黑板异或游戏
2021-05-22 LeetCode每日一题
链接:https://leetcode-cn.com/problems/chalkboard-xor-game/
标签:数学、异或 题目 黑板上写着一个非负整数数组 nums[i] 。Alice 和 Bob 轮流从黑板上擦掉一个数字,Alice 先手。如果擦除一个数字后…
1442. 形成两个异或相等数组的三元组数目
2021-05-18 LeetCode每日一题
链接:https://leetcode-cn.com/problems/count-triplets-that-can-form-two-arrays-of-equal-xor/
标签:数组、位运算、数学 题目 给你一个整数数组 arr 。
现需要从数组中取三个下标 i、j 和 k ,其中 (0 <…
19. 概率与统计 - 频率派贝叶斯派
文章目录 频数和频率频率派视角下的概率贝叶斯派视角下的概率Hi, 您好。我是茶桁。
本节课,咱们开始学习「概率&统计」的部分,说实话,这个部分是我觉得最有意思的地方。
在之前的课程中,除了导论课给大家过了一遍通识性的各个领域的一些知识之外,我们已经上过了关于…
【力扣周赛】第 363 场周赛(完全平方数和质因数分解)
文章目录 竞赛链接Q1:100031. 计算 K 置位下标对应元素的和竞赛时代码写法2——手写二进制中1的数量 Q2:100040. 让所有学生保持开心的分组方法数(排序后枚举分界)竞赛时代码 Q3:100033. 最大合金数(二分答…
测度上Lebesgue积分的确定
本文假定读者有基本的测度论知识,故仅对测度做简单介绍. Definition 1 \text{Definition 1 }Definition 1 集合XXX的子集族τ\tauτ称为拓扑,若τ\tauτ满足(1)∅,X∈τ\varnothing ,X\in \tau∅,X∈τ;(2)可列元素的交的封闭性;(3)有限、可列、或不可列元素的并的封闭性. 这样…
卷积和拉普拉斯变换的关系-卷积定理
还可以见: https://www.cnblogs.com/xml299792458/p/15143068.html https://zhuanlan.zhihu.com/p/152647974 https://zhuanlan.zhihu.com/p/128812880?ivk_sa1024320u
http://howellkb.uah.edu/public_html/DEtext/Part4/Inverse_Laplace.pdf#:~:textThe%20Inver…
Synchronicity
题目描述 大家知道什么叫做Synchronicity吗,其中文翻译为“共时性”,这是荣格对一些超自然的现象做出的解释。这些现象包括“说曹操曹操到”,“噩梦成真”等……说这么学术干嘛?Synchronicity不就是LMZ最爱的一首歌嘛!…
通过描述系统的微分方程,判断系统是否为线性系统以及是定常系统还是时变系统
目前只写了叠加性部分,齐次性、定常时变类似(之后补) 如果不是微分方程中含有积分,那么两边微分/求导消去积分 目录线性系统叠加性定义判断方法例题齐次性定义判断方法例题非线性系统定常系统线性定常系统时变系统线性时变系统线性…
一道求导题:1004T3
需要知识: ( x n ) ′ n x n − 1 (x^n)nx^{n-1} (xn)′nxn−1 ( s i n x ) ′ c o s x (sinx)cosx (sinx)′cosx [ f ( g ( x ) ) ] ′ f ′ ( g ( x ) ) g ′ ( x ) [f(g(x))]f(g(x))\times g(x) [f(g(x))]′f′(g(x))g′(x)
推完之后,考虑导函数与x轴的交点…
【数学 与 算法】卡特兰数 - 有多少种出栈情况?等
感想 体现的数学思想丰富:【抽象的艺术】数学真是一个神奇的东西。一个卡特兰数居然有如此广泛的应用,抽象概括了如此多的现实状况。(体会到了一些递推数列的价值) 【卡特兰数的应用】凸包的多边形划分、矩阵的连乘的数目、括号匹…
关于机器学习的一些数学基础(二)
一般在我们刚接触机器学习的算法时,我们要让机器去学习东西,那么就需要让机器在学习的过程中修正自己的参数。一般在无约束优化问题时,梯度下降(Gradient Descent)是最常采用的方法之一。一般我们用下山法来通俗的解说…
2020 ICPC·小米邀请赛 决赛 Rikka with Composite Number
原题链接 题意
给定一个集合D{1,2,3,4,5,6,7,8,9},一个数C0,执行操作 CC10d(集合D中的一个数,选中的概率相同)࿰…
牛客练习赛75 A题 数论签到
原题链接 思路 1.这属于数论签到题,但是一上去就wa了一发,因为在算fn时进行了mod p 操作 ,改变了最终的结果 2.这到题主要用到快速幂和费马小定理 3.计算fn时肯定是要取模的,但是绝对不是模p,根据费马小定理推导&#…
AcWing 每日一题 2022/5/4【2031. 折叠绳子】
AcWing 每日一题 2022/5/4【2031. 折叠绳子】
农夫约翰有一条长度为 L 的绳子,可用于农场周围的各种任务。
绳子在不同的位置有 N 个绳结,包括两个端点处各有一个。
约翰注意到,在某些位置,他可以将绳子对折,这样&a…
2875. 超级胶水(数学归纳)【第十一届蓝桥杯省赛第一场C++A组】
2875. 超级胶水
小明有 n 颗石子,按顺序摆成一排。
他准备用胶水将这些石子粘在一起。
每颗石子有自己的重量,如果将两颗石子粘在一起,将合并成一颗新的石子,重量是这两颗石子的重量之和。
为了保证石子粘贴牢固,粘…
求素数(质数)算法的N种境界 - 试除法和初级筛法
版权声明 本博客所有的原创文章,作者皆保留版权。转载必须包含本声明,保持本文完整,并以超链接形式注明作者编程随想和本文原始地址:http://program-think.blogspot.com/2011/12/prime-algorithm-1.html
★引子 前天,…
【题解】震惊!!!GCD SUM套路竟狂水七倍经验!!!
标题党又来了
题目描述
给定nnn,求∑i1n∑ji1ngcd(i,j)\sum\limits_{i1}^{n} \sum\limits_{ji1}^{n}gcd(i,j)i1∑nji1∑ngcd(i,j)。 解法1:暴力
两个for搞定。每一次计算复杂度为O(n2)O(n^2)O(n2)。
于是你可以水掉UVA11417。
解法2&…
数学分析第五课(关于实数的4个定理)
We will introduce four theorems in R\mathbb{R}R, and they are such obvious that you even don’t realise that they need proofs.
Theorem 1: If x∈R,y∈Rx\in \mathbb{R}, y\in \mathbb{R}x∈R,y∈R and x>0x>0x>0, then there is a positive integer nnn su…
数学分析第三课(上下确界的概念)
Definition Let SSS be a set. An order on SSS is a relation, denote by <<<, with the following two properties: If x∈Sx\in Sx∈S and y∈Sy\in Sy∈S then one and only one of the statements x<y,xy,y<xx<y, xy, y<xx<y,xy,y<x is true. …
数学分析第一课(数学分析和微积分的桥梁)
What is the foundation of differential calculus? We will discover it from one of the most important theorem in differential calculus which called Mean-Value theorem. In order to prove this theorem, we only need several steps. THEOREM 1—The Extreme Value …
裴礼文《数学分析中的典型问题与方法》P31~60
裴礼文《数学分析中的典型问题与方法》
第2天31~60
第1章 一元函数极限
3.求极限值的若干方法
利用等价代换和初等变形求极限。 等价代换。 先求出可以求出来的值。根号内最好转变为一个常数和一个分式的和。等价无穷小代换。注意只有在x出现的时候才可以用,如果…
计算机视觉基础 (3)-坐标变换
图像处理、立体视觉等等方向常常涉及到四个坐标系:世界坐标系、相机坐标系、图像坐标系、像素坐标系。例如下图: 图中主要涉及到4个坐标:
1. 世界坐标系与相机坐标系 从世界坐标系变换到相机坐标系属于刚体变换:即物体不会发生形变,只需要进…
LintCode 2.尾部的零
设计一个算法,计算出n阶乘中尾部零的个数 样例 11! 39916800,因此应该返回 2 思路: 1 * 2 * 3 * 4 * ......* N中每一个因数分解因子,结果:1 * 2 * 3 * (2 * 2) * 5 * (2 * 3) *7 * (2 * 2 *2) *......10进制数结尾每…
拉普拉斯算子原理 图像增强
数学基础 拉普拉斯算子,二阶微分线性算子,为什么上来就学二阶微分算子,前文说过,与一阶微分相比,二阶微分的边缘定位能力更强,锐化效果更好,所以我们来先学习二阶微分算子,使用二阶微…
线性代数的学习和整理---番外1:EXCEL里角度,弧度,三角函数
目录
1 角的度量:角度和弧度
1.1 角度 angle
1.1.1 定义
1.1.2 公式
1.1.2 角度取值范围
1.2 弧长和弦长
1.3 弧度 rad
1.3.1 弧长和弧度定义的原理
1.3.2 定义
1.3.3 取值范围
1.3.4 取值范围
1.4 角度,弧度的换算
1.5 EXCEL里进行角度和…
【Leetcode】118.杨辉三角
一、题目
1、题目描述
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。 示例1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]示例2:
输入: numRows = 1
输出: [[1]]提示: …
【线性代数/机器学习】矩阵的奇异值与奇异值分解(SVD)
文章目录 一、引言二、奇异值三、奇异值分解的定义四、如何进行奇异值分解参考资料 一、引言
我们知道,对于一个 n n n\times n nn的矩阵 A A A,如果 A A A有 n n n个线性无关的特征向量,则 A A A可以相似对角化,即存在可逆矩阵…
2651. 计算列车到站时间
文章目录 Tag题目来源题目解读解题思路方法一:数学 知识回忆除法运算 写在最后 Tag
【数学】 题目来源
2651. 计算列车到站时间 题目解读
给你一个列车预计到达时间点和一个列车延误的时间,请返回列车实际的到达时间。 解题思路
方法一:数…
裴礼文《数学分析中的典型问题与方法》 P1~31
裴礼文《数学分析中的典型问题与方法》
第1天:1~31
第1章 一元函数极限
函数 关于反函数 只要是有f゜f⁻(),结果都为括号里的值复合函数的反函数公式奇函数、偶函数 整体的思想和反函数中第1条的思想。例1.1.4任意对称区间上的任意函数总可以表示成一个偶函数与一…
第一章 概率与统计介绍--机器学习数学基础
第一章 概率与统计介绍–机器学习数学基础 1.1 简介 概率与统计 Lary Wasserman 在《All of Statistics》
概率:The basic problem that we study in probability is: Given a data generating process, what are the properties of the outcomes? 例如࿱…
剑指 offer acwing 25 剪绳子 (数学)
题面 题解 这是一道经典的数学结论问题,先说结论,就是我们剪的长度只有2和3两种,而且2最多为2个,当绳子的长度模3余1时,绳子长度为2个2,其余都是3;模3余2时,有一段是2,其…
群环域,理想商环,原根复习
包含了抽象代数里面的一些概念,最近看文章的时候一直反映不过来,理想是个啥来着,环和域的区别是啥来着。所以统筹整理一下。 文章目录集合/(Set):半群/(Monoid):群(G,⋅)(G,\cdot)(G,⋅)/(Group):交换群/(C…
算法竞赛进阶指南---0x05(排序)七夕祭
题面 题解 我们可以发现,通过行与行(上下)交换,对列无影响,列与列(左右)交换,对行无影响 。也就是说行与列的交换是相互独立的,那么求总的交换次数最小就可以变成求行与列…
JAVA-Math类
关于数学相关的一个类,主要包含了一些数学公式,求绝对值,最大值最小值,和堆角度的操作的方法。
(Math.cbrt(27));//立方根
double result 0;
result Math.ceil(2.2);//天花板,返回大于等于实际参数的正整数的值
resu…
西南科技大学第十六届ACM程序设计竞赛暨绵阳市邀请赛 E 呼兰河传
题面 题解 思路很简单,但是易错点较多,赛事wa了10多发,心态有点炸题中要求最小公倍数最大,肯定是所有数的最小公倍数才会最大可以把所有数的因子求出来,然后进行乘积,注意优化,具体看代码 代码 …
codeforces 1475 E Advertising Agency (组合数)
题面 题意
t组样例,每组n个数,给定一个k,问选取k个数组成最大的值,有多少种组合方案
思路 E题比D题简单太多,一定要先看数据范围啊!!!!,数据范围很小&#…
EP6: Wythoff’s Game (威佐夫博弈)
此篇为转载,做收藏之用,以下是作者的版权信息: 版权声明:转载时请以超链接形式标明文章原始出处和作者信息及本声明 http://www.blogbus.com/yjq24-logs/42653430.html 大致上是这样的:有两堆石子,不妨先认…
【洛谷】P1163 银行贷款
原题链接:https://www.luogu.com.cn/problem/P1163
目录
1. 题目描述
2. 思路分析
3. 代码实现 1. 题目描述 2. 思路分析
这题需要注意的是利率按月累计这句话,也就是相当于“利滚利”。
我们定义sum变量表示贷款原值,money表示每月支付…
μ^2的根号暴力计算方法
上结论: 左边式子的本质就是 n n n 以内有多少个数没有平方因子
然后我们枚举所有平方因子 i 2 i^2 i2,包含它的有 n i 2 \Large\frac {n}{i^2} i2n 个
右边本质是一个容斥,首先所有数都有平方因子 1 2 1^2 12,然后类似 …
G. Best ACMer Solves the Hardest Problem
Problem - G - Codeforces 有一天,一位优秀的ACMer将离开这个领域,面对新的挑战,就像前辈们所做的一样。他们中的一些人接管了家族企业,一些人在失业的边缘挣扎。一些人有勇气展示自己,成为专业的Ingress玩家ÿ…
LeetCode 2591. 将钱分给最多的儿童
【LetMeFly】2591.将钱分给最多的儿童
力扣题目链接:https://leetcode.cn/problems/distribute-money-to-maximum-children/
给你一个整数 money ,表示你总共有的钱数(单位为美元)和另一个整数 children ,表示你要将…
【AI数学】N choose K
今天读论文读到了"N choose K"这个概念,查询以后顺便用博客记录一下~ N choose K表示在N个对象中选K个对象一共有多少种选法,一般表示为 C ( N , K ) C(N,K) C(N,K)。也就是咱们高中学的: C N K N ! ( N − K ) ! K !…
【数学知识】一些数学知识,以供学习
矩阵的特征值和特征向量 https://zhuanlan.zhihu.com/p/104980382
矩阵的逆 https://zhuanlan.zhihu.com/p/163748569
对数似然方程(log-likelihood equation),简称“似然方程”: https://baike.baidu.com/item/%E5%AF%B9%E6%95%B0%E4%BC%BC%E7%84%B6%E6%96%B9%E7…
SEAL:RLWE-BFV 开源算法库
参考文献:
GitHub - microsoft/SEAL: Microsoft SEAL is an easy-to-use and powerful homomorphic encryption library.[HS13] Halevi S, Shoup V. Design and implementation of a homomorphic-encryption library[J]. IBM Research (Manuscript), 2013, 6(12-15…
5.3每日一题(不确定正负号的级数敛散性:和一个正项级数比较判定)
比较判别法和比较判别法的极限形式是对正项级数而言的,若一个级数和p级数比较,结果>0,则同敛散;若结果<0,则结果乘以-1 结果又同敛散了;所以只要比值不等于0,则同敛散;
所以当…
3.12每日一题(有理函数不定积分)
两种方法: 1、拆项,然后分别加项减项拆,把分母降幂 注: x凑x的平方时前面要乘1/2 分子为x的平方可以分一个x去凑x的平方 2、联想三角有理函数公式,使用三角函数求解 用tant替换x;再通过二倍角公式降幂即可 …
3.15每日一题(分部积分求不定积分)
解法一:令lnx等于t;求出x与t的关系,带入f(lnx)的式子中;通过凑微分,分部积分等方法求出答案
注:在分部积分后,求不定积分时 (1)可以加项减项拆的方法求(常规…
力扣第96题 不同的二叉搜索树 c++ 二叉搜索树 动态规划 + 数学思维
题目
96. 不同的二叉搜索树
中等
相关标签
树 二叉搜索树 数学 动态规划 二叉树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: 输入&#…
3.20每日一题(分部积分、换元求定积分)
类型多项式的n次幂:
方法一: 展开然后求积分
方法二: 换元,令x-1t,再展开
方法三: 把一个整体凑到dx,再分部积分;如把(x-1)的n次幂凑到dx,分部…
3.21每日一题(区间在现求定积分)
当发现一个定积分,原函数根本找不出来时,可以用变量代换:区间再现!!!
数学概率 | 旋转矩阵、欧拉角、四元数
目录
一,旋转矩阵
二维旋转矩阵
三维旋转矩阵
二,欧拉角
三,四元数
四,矩阵、欧拉角、四元数相互转换
四元数转矩阵
矩阵转四元数
欧拉角转矩阵
矩阵转欧拉角
欧拉角转四元数
四元数转欧拉角 一,旋转矩阵 …
学习编程语言需要具备哪些数学基础?
学习编程语言需要具备的数学基础是一个非常广泛和深入的话题。
在计算机科学和软件工程领域,数学与编程语言密不可分,其中包括离散数学、统计学、算法分析等领域。
这里将从以下四个方面详细论述学习编程语言需要具备的数学基础:基本数学知…
codeforces 185B Mushroom Scientists【不等式的应用】
题目分析 xa∗yb∗zcaa∗bb∗cc∗(xa)a∗(yb)b∗(zc)cx^a*y^b*z^c a^a*b^b*c^c*(\frac{x}{a})^a *(\frac{y}{b})^b*(\frac{z}{c})^cxa∗yb∗zcaa∗bb∗cc∗(ax)a∗(by)b∗(cz)c ≤aa∗bb∗cc∗(a∗xab∗xbc∗xcabc)(abc)\le a^a*b^b*c^c*(\frac{a*\frac{x}{a}b*\frac{x}{…
2019数二(二重积分的不等式问题)
注: 1、在相同积分区域内的积分比较大小:被积函数大的积分值大,被积函数小的积分值小 2、在区间[0,Π/2]上 :sinx < x < tanx
数学概念 | 旋转矩阵、欧拉角、四元数
目录
一,旋转矩阵
二维旋转矩阵
三维旋转矩阵
二,欧拉角
三,四元数
四,矩阵、欧拉角、四元数相互转换
四元数转矩阵
矩阵转四元数
欧拉角转矩阵
矩阵转欧拉角
欧拉角转四元数
四元数转欧拉角 一,旋转矩阵 …
《线性代数》 李炯生\查建国\王新茂 中国科学技术大学 第2版 部分习题答案
百度了一圈没有靠谱点的答案,于是便有了这篇博客。 只写了一些自己觉得有价值的习题。 文章目录第一章 多项式1.3 整除性与最大公因式习题3习题101.5 实系数与复系数多项式习题1习题2.(4)习题101.6 整系数与有理系数多项式例1例2习题2习题6习题7习题81.8 对称多项式…
伊恩·斯图尔特《改变世界的17个方程》波动方程笔记
主要是课堂的补充(yysy,我觉得课堂的教育模式真有够无聊的,PPT、写作业、考试,感受不到知识的魅力。 它告诉我们什么? 小提琴琴弦上某个小段的加速度,与相邻段相对于该段的平均位移成正比。 为什么重要&…
有趣的数学 sign是什么函数
在数学中,函数sign指的是符号函数,它的定义如下:对于任意实数x,若x>0,则sign(x)1;若x0,则sign(x)0;若x<0,则sign(x)-1;简单来说,sign函数就…
3.29每日一题(微分方程的几何应用题:重点考察)
1、画图,把题目中的条件标出来
2、通过题目中的条件设出正确的微分方程(解题的关键) 注:用点斜式设方程的时候,注意Y - y y(X - x)中(x,y)为曲边上的动点&a…
易错知识点(数学一)
一、反常积分判敛 1、构造使其极限等于一个大于0的常数 1)前者通过:化等价无穷小 or 泰勒展开 2)若存在p>1使得等式成立,则收敛 考察形式:1、已知收敛,求f(x)中的幂次取值范围 主要思想:比较…
Jacobi迭代法和Gauss-Seidel迭代法的收敛性
Axb
系数矩阵A按行严格对角占优
若系数矩阵A按行严格对角占有>Jacobi迭代法和Gauss-Seidel迭代法均收敛
迭代矩阵B谱半径<1
Jacobi迭代法和Gauss-Seidel迭代法收敛<>迭代矩阵B的谱半径<1 其中,Jacobi迭代法的迭代矩阵 B − D − 1 ( L U ) B-D…
3.30每日一题(多元函数微分学)
1、判断连续:再分界点的极限值等于该点的函数值; 如何求极限值: 初步判断:分母都为二次幂开根号,所以分母为一次幂;分子为二次,一般来说整体为0;
如何说明极限为零(常用…
FFT/NTT:以 CRT 的视角
参考文献
[CT65] Cooley J W, Tukey J W. An algorithm for the machine calculation of complex Fourier series[J]. Mathematics of computation, 1965, 19(90): 297-301.[Ber01] Bernstein D J. Multidigit multiplication for mathematicians[J]. Advances in Applied Mat…
HDRP图形入门:HDRP渲染管线depth翻转
新项目开坑HDRP渲染管线,花了些时间把项目开发框架和图形工作流更新到最新版本,其间发现HDRP中深度信息和buildin渲染管线翻转了。 以前的buildin渲染管线,距离摄像机越近depth->0,越远depth->1,这也很好理…
C++二分查找算法:132 模式
说明
本篇是视频课程的讲义,可以看直接查看视频。也可以下载源码,包括空源码。 题目
给你一个整数数组 nums ,数组中共有 n 个整数。132 模式的子序列 由三个整数 nums[i]、nums[j] 和 nums[k] 组成,并同时满足:i &l…
三国杀中的概率学问题4——曹冲
前言
这篇文章是围绕曹冲的称象技能展开的一些数学上的讨论,将涉及到积分、概率论等知识,并会做很多拓展。 值得说明的是,本文受到了这篇文章的一些启发。
连续情形1
先来看一个连续情形的问题。 问题一:假设每张牌的点数是0~1…
acwing算法基础之数学知识--扩展欧几里得算法
目录 1 基础知识2 模板3 工程化 1 基础知识
数学定理:对于任意正整数a和b,一定存在非零整数x和y,使得xaybgcd(a,b)。
扩展欧几里得算法的关键步骤:
如果b为0,那么可取x 1, y 0。否则,exgcd(b, a % b)&…
快速乘法技巧:Karatsuba, Toom, Good, Schonhage, Strassen, Nussbaumer
参考文献:
[Ber01] Bernstein D J. Multidigit multiplication for mathematicians[J]. Advances in Applied Mathematics, 2001: 1-19.FFT/NTT:以 CRT 的视角 文章目录 Map & LiftMappingLifting Karatsuba’s trickToom’s trickFFT trickGood’s…
【面试经典150 | 数学】回文数
文章目录 写在前面Tag题目来源题目解读解题思路方法一:反转一半数字 其他语言python3 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本…
LeetCode 2731. 移动机器人:脑筋急转弯
【LetMeFly】2731.移动机器人
力扣题目链接:https://leetcode.cn/problems/movement-of-robots/
有一些机器人分布在一条无限长的数轴上,他们初始坐标用一个下标从 0 开始的整数数组 nums 表示。当你给机器人下达命令时,它们以每秒钟一单位…
人工智能在教育上的应用2-基于大模型的未来数学教育的情况与实际应用
大家好,我是微学AI ,今天给大家介绍一下人工智能在教育上的应用2-基于大模型的未来数学教育的情况与实际应用,随着人工智能(AI)和深度学习技术的发展,大模型已经开始渗透到各个领域,包括数学教育。本文将详细介绍基于大模型在数学…
Multi-value PBS
参考文献:
[CIM19] Carpov S, Izabachne M, Mollimard V. New techniques for multi-value input homomorphic evaluation and applications[C]//Topics in Cryptology–CT-RSA 2019: The Cryptographers’ Track at the RSA Conference 2019, San Francisco, CA, …
5人雨天参会,每人带一把伞,入场时随意挂在架子上,离场时每人随意拿走一把。求:
(1) 每人拿的都不是自己原伞的排列数?
(2) 至少一人拿到自己原伞的概率? 解:
(1) 5人错位排序 (2)
即全排列数减去5人错排的概率,为: 或从另一个角度考虑,即5人中最多有四人错排,
其概率为 …
LeetCode-48. 旋转图像【数组 数学 矩阵】
LeetCode-48. 旋转图像【数组 数学 矩阵】 题目描述:解题思路一:一行代码!Python zip函数图一乐【zip函数实现主对角线翻转,[::-1]实现垂直翻转】解题思路二:其实我们也可以先水平轴翻转,让后主对角线翻转。…
数论与线性代数——整除分块【数论分块】的【运用】【思考】【讲解】【证明(作者自己证的QWQ)】
文章目录 整除分块的思考与运用整除分块的时间复杂度证明 & 分块数量整除分块的公式 & 公式证明公式证明 代码code↓ 整除分块的思考与运用
整除分块是为了解决一个整数求和问题 题目的问题为: ∑ i 1 n ⌊ n i ⌋ \sum_{i1}^{n} \left \lfloor \frac{n}{…
OpenFOAM学习笔记
OpenFOAM
计算流体力学:用计算机求解流体控制方程,来模拟真实情况下,流体的流动状态OpenFOAM的离散方法:有限体积法,将整个空间划分成若干个控制体OpenFOAM使用的网格系统:同位网格(Collocated…
【Image】GAN的超详细解释(以及奇怪的问题)
GAN原理
工作流程
下面是生成对抗网络(GAN)的基本工作原理 在GAN的架构中,有两个关键的组件:生成器(Generator)和鉴别器(Discriminator)。 生成器(Generator࿰…
生活中的数学 --- 等额本息贷款和等额本金贷款的月供应该怎么算?
等额本息贷款和等额本金贷款的月供应该怎么算? 从一个例子开始,假设我要从银行贷款36万(即,本金),银行给出的贷款年利率是12%(月利率为年利率除以12),贷款半年(6个月),按月还款,分6期还完。 问分…
算法题中常用数学概念、公式、方法汇总(其四:组合学)
文章目录 组合学加法原理乘法原理排列组合组合恒等式二项式定理 华为OD算法/大厂面试高频题算法练习冲刺训练 组合学
加法原理
加法原理是指做一件事情,完成它有n类方式,第一类方式有M1种方法,第二类方式有M2种方法,以此类推&am…
Large-Precision Sign using PBS
参考文献:
[CLOT21] Chillotti I, Ligier D, Orfila J B, et al. Improved programmable bootstrapping with larger precision and efficient arithmetic circuits for TFHE[C]//Advances in Cryptology–ASIACRYPT 2021: 27th International Conference on the T…
【每日一题】一周中的第几天
文章目录 Tag题目来源解题思路方法一:模拟 写在最后 Tag
【模拟】【数学】【2023-12-30】 题目来源
1185. 一周中的第几天 解题思路
方法一:模拟
思路
题目中的日期是在 1971 到 2100 年之间的有效日期,即 1971-01-01 到 2100-12-31 范围…
【动态规划】C++ 算法458:可怜的小猪
作者推荐
视频算法专题
涉及知识点
动态规划 数学
力扣458:可怜的小猪
有 buckets 桶液体,其中 正好有一桶 含有毒药,其余装的都是水。它们从外观看起来都一样。为了弄清楚哪只水桶含有毒药,你可以喂一些猪喝,通过观察猪是否…
约数个数和约数之和算法总结
知识概览
约数个数 基于算数基本定理,假设N分解质因数的结果为 可得对于N的任何一个约数d,有 因为N的每一个约数和~的一种选法是一一对应的,根据乘法原理可得, 一个数的约数个数为 约数之和 一个数的约数之和公式为 多项式乘积的…
【上分日记】第369场周赛(分类讨论 + 数学 + 前缀和)
文章目录 前言正文1.3000. 对角线最长的矩形的面积2.3001. 捕获黑皇后需要的最少移动次数3.3002. 移除后集合的最多元素数3.3003. 执行操作后的最大分割数量 总结尾序 前言 终于考完试了,考了四天,也耽搁了四天,这就赶紧来补这场周赛的题了&a…
自动驾驶 | 决策规划岗位校招面试中常见的数学方法整理
文章目录 前言计算几何学求解方程的根无约束优化——求解函数极值 前言
前段时间,我mentor面试了一个决策规划方向实习的候选人,这个候选人是我母校的学生,算是我的学弟,跟我一个专业,他的老师是我学院的院长…
【数位dp】【C++算法】600. 不含连续1的非负整数
作者推荐
【矩阵快速幂】封装类及测试用例及样例
涉及知识点
数位dp
LeetCode600. 不含连续1的非负整数
给定一个正整数 n ,请你统计在 [0, n] 范围的非负整数中,有多少个整数的二进制表示中不存在 连续的 1 。 示例 1: 输入: n 5 输出: 5 解释: 下…
【动态规划】【滑动窗口】【C++算法】 629K 个逆序对数组
作者推荐
【矩阵快速幂】封装类及测试用例及样例
本文涉及知识点
动态规划 C算法:滑动窗口总结
LeetCode629: K 个逆序对数组
逆序对的定义如下:对于数组 nums 的第 i 个和第 j 个元素,如果满足 0 < i < j < nums.length 且 nu…
C#,入门教程(66)——枚举Enum的高等用法
前言:国内码农与国外优秀程序员的最大区别是,我们的专家、教授喜欢唾沫横飞地,夸夸其谈语言特性、框架、性能,唯一目的是带私货(书籍或教程),很少能写出真有用的程序。差距在哪呢?基…
【工具】SageMath|Ubuntu 22 下 SageMath 极速安装 (2024年)
就一个终端就能运行的东西, 网上写教程写那么长, 稍微短点的要么是没链接只有截图、要么是链接给的不到位, 就这,不是耽误生命吗。
废话就到这里。 文章目录 链接步骤 链接 参考: Install SageMath in Ubuntu 22.04We…
备战蓝桥杯---数学基础1
质数的性质:
1.n>3,n与n1必然有一个不是质数。
2.质数有无穷多个:
如果有限个,那么他们的乘积1必然也是质数,矛盾。
3.存在任意长的一段连续的数都是合数。
我们令长度为n,构造a(n1)!,则(a2)%20,(a3)%30......(an1)%(n1)0…
备战蓝桥杯---组合数学基础1
让我们来几道高中的组合题吧: 1.我们一定有n个向下,为
2.我们挑最大的两个,条件是他们奇偶性相同,为2*A10,2;
3.用捆绑法即可。 4.我们用隔板法,为
5.问题等价于23个相同的球放到3个盒子里,每个盒子至少…
备战蓝桥杯---组合数学2
本专题主要介绍容斥原理。
大家高中的时候肯定接触过韦恩图,容斥原理比较通俗的理解就是减去所有可能并加上重叠的部分。
我们直接看公式: 知道后,我们先看道模板题: 下面是AC代码:
#include<bits/stdc.h>
us…
(done) 两个矩阵 “相似” 是什么意思?
参考视频:https://www.bilibili.com/video/BV1zu411673J/?spm_id_from333.337.search-card.all.click&vd_source7a1a0bc74158c6993c7355c5490fc600
参考资料:https://baike.baidu.com/item/%E7%9B%B8%E4%BC%BC%E7%9F%A9%E9%98%B5/10369874?frge_a…
位姿变换线性变换与坐标变换
位姿,线性变换与坐标变换.yuque
内旋,外旋, 左乘,右乘很容易把人绕晕是因为缺少一种科学的符号。 自己的符号,如果经常变不稳定,对推理和理解都很不利。 一旦问题复杂起来, 直观和直觉靠不住, 只能靠代数符号来推理 约定 P1: A,B,C…是空间中的标准正交基 P2: [a1,…
NTT 的各类优化:Harvey、PtNTT,Intel AVX2、ARM Neon、GPGPU
参考文献:
[Har14] Harvey D. Faster arithmetic for number-theoretic transforms[J]. Journal of Symbolic Computation, 2014, 60: 113-119.[Sei18] Seiler G. Faster AVX2 optimized NTT multiplication for Ring-LWE lattice cryptography[J]. Cryptology ePr…
用分布函数定义的随机变量的独立性的合理性
随机变量的独立性是这样定义的:
如果对任意 x , y x, y x,y 都有 P { X ≤ x , Y ≤ y } P { X ≤ x } P { Y ≤ y } P\{X\leq x,Y\leq y\} P\{X\leq x \}P\{Y\leq y\} P{X≤x,Y≤y}P{X≤x}P{Y≤y} 即 F ( x , y ) F X ( x ) F Y ( y ) F(x,y)F_X(x)F_Y(y) F…
【数学】【C++算法】780. 到达终点
作者推荐
视频算法专题
本文涉及知识点
数学
LeetCode780. 到达终点
给定四个整数 sx , sy ,tx 和 ty,如果通过一系列的转换可以从起点 (sx, sy) 到达终点 (tx, ty),则返回 true,否则返回 false。 从点 (x, y) 可以转换到 (x…
《洛谷深入浅出进阶篇》模意义下的乘法逆元+洛谷P3811
什么是乘法逆元?
算数意义上的乘法逆元指的是倒数,即:a*(1/a)1
所以 1/a 是 a在算数意义下的乘法逆元,或者可以说二者互为逆元。 这有什么用呢?
除以a就等于乘上a的乘法逆元,乘以…
Hardness of Scheme-Switching and Comparison in FHE
参考文献:
[AP13] Alperin-Sheriffff, J., Peikert, C.: Practical bootstrapping in quasilinear time. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 1–20. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-…
C++二分查找算法:132 模式解法二枚举2
题目及解法一:
https://blog.csdn.net/he_zhidan/article/details/134362273
分析
第一步,选择各3对应的1,如果有多个符合对应最小的1,记录num[0,j)中的最小值iMin,如果nums[j]大于iMin,则m3To1 [nums[j…
【文末送书——数学经典著作】工科必备的数学思维培养
欢迎关注博主 Mindtechnist 或加入【智能科技社区】一起学习和分享Linux、C、C、Python、Matlab,机器人运动控制、多机器人协作,智能优化算法,滤波估计、多传感器信息融合,机器学习,人工智能等相关领域的知识和技术。关…
FO with Prefix Hashing KEM Generalizations
参考文献:
[Has88] Hastad J. Solving simultaneous modular equations of low degree[J]. siam Journal on Computing, 1988, 17(2): 336-341.[BBM00] Bellare M, Boldyreva A, Micali S. Public-key encryption in a multi-user setting: Security proofs and im…
4.6每日一题(多元函数的隐函数求导)
三元方程确定的二元函数类型的隐函数
方法一:两边对x求偏导,把y看成常数 注:z可以把x和y同时代入求出答案
方法二:带公式
信息工程大学第五届超越杯程序设计竞赛(同步赛)题解
比赛传送门
博客园传送门
c 模板框架
#pragma GCC optimize(3,"Ofast","inline")
#include<bits/stdc.h>
#define rep(i,a,b) for (int ia;i<b;i)
#define per(i,a,b) for (int ia;i>b;--i)
#define se second
#define fi first
#define e…
【位运算】【脑筋急转弯】2749. 得到整数零需要执行的最少操作数
作者推荐
视频算法专题
本文涉及知识点
2749. 得到整数零需要执行的最少操作数
给你两个整数:num1 和 num2 。 在一步操作中,你需要从范围 [0, 60] 中选出一个整数 i ,并从 num1 减去 2i num2 。 请你计算,要想使 num1 等于 …
Python数值和符号算法计算及3D视图物理数学波形方程
要点
Python数值和符号计算及3D可视化以下物理方程: 物理数学方程分析:二分算法和牛顿-拉夫森算法解方程根。最小二乘法拟合方程和数据。短期傅里叶变换和小波分析非平稳信号。使用主成分分析复杂和大型数据集,提取时空相关性,分…
LeetCode题练习与总结:Pow(x, n)
一、题目描述
实现 pow(x, n) ,即计算 x 的整数 n 次幂函数(即,x^n )。 示例 1:
输入:x 2.00000, n 10
输出:1024.00000示例 2:
输入:x 2.10000, n 3
输出&#x…
[LeetCode][LCR131]砍竹子 I——推测规律
题目
LCR 131. 砍竹子 I 现需要将一根长为正整数 bamboo_len 的竹子砍为若干段,每段长度均为正整数。请返回每段竹子长度的最大乘积是多少。 示例 1: 输入: bamboo_len 12 输出: 81 提示: 2 < bamboo_len < 58 注意:本题…
【字符串】【分类讨论】【KMP】1163. 按字典序排在最后的子串
作者推荐
视频算法专题
本文涉及知识点
字符串 字典序 分类讨论 本题无法使用KMP,因为t1不段变化。
LeetCode1163. 按字典序排在最后的子串
给你一个字符串 s ,找出它的所有子串并按字典序排列,返回排在最后的那个子串。 示例 1…
LeetCode 1954. 收集足够苹果的最小花园周长:数学O(1)的做法
【LetMeFly】1954.收集足够苹果的最小花园周长:数学O(1)的做法
力扣题目链接:https://leetcode.cn/problems/minimum-garden-perimeter-to-collect-enough-apples/
给你一个用无限二维网格表示的花园,每一个 整数坐标处都有一棵苹果树。整数…
汤姆·齐格弗里德《纳什均衡与博弈论》笔记(7)博弈论与概率论
第十一章 帕斯卡的赌注——博弈、概率、信息与无知 在与费马就这个问题的通信过程中,帕斯卡创造出了概率论。另外,帕斯卡在进行严谨的宗教反思中,得出了概率这个概念,它在此几百年后,成为一个关键的、对博弈论的提出有…
(done) 如何计算 Hessian Matrix 海森矩阵 海塞矩阵
参考视频1:https://www.bilibili.com/video/BV1H64y1T7zQ/?spm_id_from333.337.search-card.all.click
参考视频2(正定矩阵):https://www.bilibili.com/video/BV1Ag411M76G/?spm_id_from333.337.search-card.all.click&vd_…
C代码快速傅里叶变换-分类和推理-常微分和偏微分方程
要点
C代码例程函数计算实现: 线性代数方程解:全旋转高斯-乔丹消元,LU分解前向替换和后向替换,对角矩阵处理,任意矩阵奇异值分解,稀疏线性系统循环三对角系统解,将矩阵从完整存储模式转换为行索…
【设计】 【数学】1622 奇妙序列
本文涉及知识点
设计 数学
LeetCode1622. 奇妙序列
请你实现三个 API append,addAll 和 multAll 来实现奇妙序列。 请实现 Fancy 类 : Fancy() 初始化一个空序列对象。 void append(val) 将整数 val 添加在序列末尾。 void addAll(inc) 将所有序列中的…
Codeforces Round 936 (Div. 2)(A,B,C,D)
比赛链接
div2一如既往的难欸。B是个前缀和加数学,一开始读假题了wa人麻了,发现读假题了人更麻了。C是个二分答案加dfs。D是位运算的题,一开始感觉很难,但是发现是思路假了,实际上并没有那么难(还是难 &am…
三国杀中的概率学问题3——王荣
前言
本文是三国杀中的概率学问题系列文章中的一篇,将详细讨论王荣吉占的期望摸牌数问题。并加上连续情形作为拓展。
值得说明的是,本文的思路受到了一篇文章的启发,在此特别鸣谢,这是文章的链接。
王荣吉占的期望摸牌数 王荣的…
对于概率论数字特征的理解
数字特征概述随机变量 常见数字特征数学期望均值方差标准差协方差相关系数协方差矩阵 参考 数字特征概述 在我们学习概率论的时候,很多时候我们不能深刻理解概率论中的数字特征所具有的含义,本文章尝试去帮助读者理解一些术语、概念。 什么是…
定积分的计算(分部积分法)
前置知识
分部积分法牛顿-莱布尼茨公式 定积分分部积分法
设 u , v u,v u,v在 [ a , b ] [a,b] [a,b]上可导,且 u ′ , v ′ u,v u′,v′在 [ a , b ] [a,b] [a,b]上连续,则 ∫ a b u ( x ) v ′ ( x ) d x u ( x ) v ( x ) ∣ a b − ∫ a b u ′ ( …
数学逻辑下的动态区间计算公式代码
pics 9 # 这里假设订单产品总数为9个# 初始化仓储处理费用
warehouse_handling_cost 0# 定义不同区间的单价和区间范围
price_per_unit [(0.81, 5), (0.65, 10), (0.57, 20), (0.49, 30), (0.41, 50)]# 遍历区间并计算费用
for price, limit in price_per_unit:if pics >…
Policy Evaluation收敛性、炼丹与数学家
完美的学习算法
昨天和同学在群里讨论DRL里bad case的问题。突然有同学提出观点:“bad case其实并不存在,因为一些算法已经理论证明了具有唯一极值点,再加上一些平滑技巧指导优化器,就必然可以收敛。”
当听到这个观点时&#x…
CF11B Jumping Jack 题解
CF11B Jumping Jack 题解 题目链接字面描述题面翻译题目简述题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 样例 #3样例输入 #3样例输出 #3 思路代码实现后继 题目
链接
https://www.luogu.com.cn/problem/CF11B
字面描述
题面翻译…
(邱维声)高等代数课程笔记:目录
(邱维声)高等代数课程笔记:目录
高等代数课程 - 邱维声
引言 高等代数的研究对象 高等代数的主线 线性空间的结构及其线性映射一元多项式环的结构及其通用性质 第1章 线性方程组的解法 1.1 解线性方程组的矩阵消元法1.2 线性方程组解的情况…
PostgreSQL中实现数学中的组合问题
记得在学《数值分析》这门课程时,其中有排列组合的相关计算。最近没有想到,自己居然在编程上需要了这个问题,需要在数据库的一张表中,找出任意n条记录的组合,判断组合后的图形是什么,也就是组合问题。从网上搜索的相关资料,发现很多是在Java或者python代码实现的。因为数…
3.3每日一题(变量可分离方程)
1、判断类型选方法:等式中分别提一个x、y出来,形成了x与y相乘的等式;为变量可分离类型
2、不一定非得把y解出来,化成上述的等式即可(为隐函数的方程解)
注:等式不定积分后记得+一个…
[Daimayuan] 一半相等(C++,数学)
给定 n n n ( n n n 为偶数)个整数数组 a 1 , a 2 , … , a n a_1,a_2,…,a_n a1,a2,…,an
考虑这样的一个 k k k,每次操作选定一个 i i i,将 a i a_i ai 减少 k k k,执行多次(可能 0 0 0 …
Exponential Loss 中的关于indicator 函数的一个恒等式
− x y 2 I ( x ≠ y ) − 1 -xy2\mathbf{ I}(x \ne y)-1 −xy2I(xy)−1
其中 I \mathbf{ I} I 是 indicator 函数, 定义域 为True ,函数值为 1 反之为 0 x,y 都 可以取值 {-1,1}
证明过程见下表:
xy左式右式-1-1-1-111-1-1-11111-111
26. 图论 - 树
文章目录 树生成树最小生成树图与人工智能人工智能数学基础Hi,你好。我是茶桁。
这一节课是我们AI秘籍整个数学篇的最后一节课。同样的,这节课的概念还是比较重要的。我们要来了解一下「树」。
树
树其实是图的一种,首先呢它是一个连通图,是一个不含圈的连通图。
什么叫…
论文笔记 | Nature 2023 FunSearch:利用大语言模型在数学科学领域探索新的发现
文章目录 一、前言二、主要内容三、总结🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 一、前言 科学中有许多难以解决的问题,这些问题难以获得确切解答,但却相对容易进行验证。在数学和计算机科学领域,这类问题被称为 NP 完全优化问题(NP-complete optimization pr…
第一类换元法专项训练习题
前置知识:第一类换元法(凑微分法)
题1: 计算∫x1x2dx\int \dfrac{x}{\sqrt{1x^2}}dx∫1x2xdx
解:原式12∫11x2d(x21)1x2C\dfrac 12\int \dfrac{1}{\sqrt{1x^2}}d(x^21)\sqrt{1x^2}C21∫1x21d(x21)1x2C 题…
2.23每日一题(反常积分收敛性的判断)
解法一:用定义(当被积函数的原函数比较好找时): 积分结果为存在则收敛,不存在则发散。 解法二:通过p积分的比较法判断敛散性: 即被积函数与p积分相比较,使得两者同敛散;再…
2.21每日一题(隐函数求导+变上限积分求导)
1、首先 t 0 时,x ? 或者 y ? 求出来
2、等式两边进行一阶求导,把一阶导函数(隐函数求导)求出来
3、等式两边再次求导,把二阶导函数(隐函数求导)求出来
注意:隐函数求导及变上…
2.19每日一题(分段函数求定积分)
注意:当x>1时需要分区间求定积分 用变上限积分的定理:如果 f(x) 连续,则 F(x) 的导数 f(x) 变上限积分的导数为 f(x)
1、先判断 f(x) 是否连续———>判断在分界点的值是否相等,相等则 f(x) 连续,则 F(x&#…
2.8每日一题(定积分比较大小)
在对称区间上的定积分比较大小,首先考虑积偶性:对称区间上被积函数如果是奇函数,则定积分值为0,如果被积函数为偶函数,则定积分值为2倍一般区间的定积分。
配置法 求解1D第二类线性的Fredholm积分方程+Python
# -*- coding: utf-8 -*-
"""Created on Sat Oct 16 19:27:08 2021Collocation_1D_Second_Fredholm_IE这是一个采用配置法 求解第二类 线性的fredholm积分方程的程序基函数采用 分片的线性基函数/帽函数u(x)-Kuf(x)Kuk(x,y)*u(y)在[a,b]上关于y的积分author: Mr…
数学回味系列之15 - 兔子繁殖问题
问题提出: 著名意大利数学家Fibonacci曾提出一个问题: 有一对小兔子,从出生两个月后(第3个月起)开始每个月都生一对兔子。 小兔子两个月后(第3个月起)开始每个月又生一对兔子。按此规律…
数学回味系列之11 - 农夫过河问题
问题提出: 对象:农夫、狼、羊、白菜 目标:农夫想划船 把狼、羊、菜和自己运到河对岸,船比较小,农夫每次只能运一种东西过河 约束条件:如果没有农夫看着,羊会偷吃菜,狼会吃羊 考虑一种…
有理函数的不定积分习题
前置知识:有理函数的不定积分
习题
计算 ∫ x 3 1 x 4 − 3 x 3 3 x 2 − x d x \int \dfrac{x^31}{x^4-3x^33x^2-x}dx ∫x4−3x33x2−xx31dx
解: \qquad 将被积函数的分母因式分解得 x 4 − 3 x 3 3 x 2 − x x ( x − 1 ) 3 x^4-3x^33x^2-xx…
数学回味系列之7 - 鸡兔同笼问题
问题提出: 鸡兔同笼,共有30个头,88只脚。求笼中鸡兔各有多少只? 来个简单的题目,陪小朋友游戏一下:) 解题思路: 从成人的角度理解,这是一个二元方程组,假设 …
数学回味系列之6 - 有趣的24点
问题提出: 从一副扑克牌里 任意取 4张牌,如何通过 加减乘除,使结果等于24? 任给4个数字 [1,13],通过 - * / 运算,使得结果 24。
解题思路: 把多元运算转化为两元运算,先从四个数…
数学回味系列之4 - 开灯关灯问题
问题提出: 有编号1~100个灯泡,起初所有的灯都是灭的。有100个同学来按灯泡开关,如果灯是亮的,那么按过开关之后,灯会灭掉。如果灯是灭的,按过开关之后灯会亮。
现在开始按开关。 第 1 个同学,把…
简单理解梯度下降法、牛顿法、高斯牛顿法、列文伯格-马夸尔特法(LM)
梯度下降法,沿着一阶导方向(雅可比矩阵)走。二维搜索问题的话可以形象理解为用平面拟合当前位置,沿着切向肯定移动最快。主要问题收敛速度慢。牛顿法,通过二阶泰勒展开求极值。二维搜索问题的话可以形象理解为用二次曲…
C++算法:第N位数的原理、源码及测试用例
本文涉及知识点 简单的数学知识。
本博文对应源码,审核比较慢,请耐心等待:https://download.csdn.net/download/he_zhidan/88504919
本博文在CSDN 学院有对应课程。 题目
给你一个整数 n ,请你在无限的整数序列 [1, 2, 3, 4, 5…
【工科数学分析】2021-10-01-工科数学分析叒复习(一)
【写东西也会感觉逐渐麻木吧,从原本的跳脱到现在的能少说就少说】
零、
数列极限的目录;
一、
数列极限的定义; 根据极限的定义联想的计算方法; 极限定义的推论; 极限的应用; 常用不等式; 常…
【复变函数】2021-09-15-复变函数/解析函数的一些想法(七)(这绝对算不上是笔记)
一
昨天看了看我自己的笔记,觉得还是那几个概念(连续,可导,可微)有种无处着力的感觉,懂了,但是没有完全懂。想起来下面还有一个解析的概念,我打算一并先做了笔记再一起对比对比&…
Matlab 自编雅可比矩阵 (jacobi) 函数与官方的Jacobian matrix(雅可比矩阵)函数对比及创新
目录0 引言1 雅可比矩阵2 matlab中函数表达式两种方法2.1 符号表达式2.2 函数句柄2.3 函数句柄与符号表达式相互转化2.4 常会用到的一些函数3 自编代码4 官方函数5 参考文献0 引言 最近遇到了一些需要求函数的雅可比矩阵的问题,例如上次发布的 blog:Matl…
leetcode.754 到达终点数字 - 数学思维
754. 到达终点数字 从1到n一直累加, 直到sumtarget, 或sum-target为偶数. 因为在第n步往回走一次,sum就会减少2n, 所以他们的差必须是偶数才能到. 本来想用前缀和找规律 但是后面发现是数学问题……好难QAQ 第一点:target正负情况是一样的,所以统一把tar…
LeetCode2444: 统计定界子数组的数目
作者推荐
【二叉树】【单调双向队列】LeetCode239:滑动窗口最大值
题目
给你一个整数数组 nums 和两个整数 minK 以及 maxK 。 nums 的定界子数组是满足下述条件的一个子数组: 子数组中的 最小值 等于 minK 。 子数组中的 最大值 等于 maxK 。 返回定界子数组的数…
第十周周赛——周赛兼组队赛第二场题解(出自 BNUOJ28207,BNUOJ28201,BNUOJ28209,codeforces 667B,HDU 5439,HDU 5478)
A题:
A题题目链接
题目描述: Star TimeLimit: 1000ms MemoryLimit:32768KB64-bit integer IO format:%I64dProblem DescriptionOverpower often go to the playground with classmates. They play and chat on the playground. One day, there are a…
导数大题练习(2023年高考真题)
已知函数 f ( x ) a ( e x a ) − x f(x)a(e^xa)-x f(x)a(exa)−x (1)讨论 f ( x ) f(x) f(x)的单调性 (2)证明:当 a > 0 a>0 a>0时,求证: f ( x ) > 2 ln a 3 2 f(x)>2\l…
HDU5621——数学应用(多边形内对角线交点个数) + 数论 + unsigned long long的应用
题目描述: KKs Point
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Submission(s): 713 Accepted Submission(s): 238 Problem DescriptionOur lovely KK has a difficult mathematical problem:He points N(2≤…
[Daimayuan] 跳跳(C++,数学)
平面上给定了一些整点(横纵坐标均为整数的点),被称为 “魔法阵”。魔法少女派派想要在各魔法阵之间传送,每一次传送,她将使用下面的方式:
刚开始,派派已经位于某传送阵之上;如果派派…
【IT】我是计算机系统大师(三)——高速缓存地址映射方式
一、前言 计算机系统结构是站在程序员的角度所看到的计算机数学,即程序员要能编写出可以在计算机上正确运行的程序必须了解概念结构和功能特性。
二、对比介绍
直接映像 图一 直接映像主存一块只能映像到Cache的一个特定块中。 1 VS 1 优点:地址变换…
随机变量的最大最小值独立性问题
作本篇的原因是下面这道题(出自2023李林6第二套) 解答:
而引发了对于随机变量的max和min值变量来说,二者是否独立的问题。推理如下:
考虑两个独立的随机变量 X , Y X, Y X,Y,变量 m , M m,M m,M为其最小…
Linear Decryption: Rate-1 FHE TLP
参考文献: [ILL89] Russell Impagliazzo, Leonid A. Levin, and Michael Luby. Pseudo-random generation from oneway functions (extended abstracts). In 21st Annual ACM Symposium on Theory of Computing, pages 12–24, Seattle, WA, USA, May 15–17, 1989.…
CSDN编程题-每日一练(2023-08-19)
CSDN编程题-每日一练(2023-08-19) 一、题目名称:风险投资二、题目名称:幼稚班作业三、题目名称:韩信点兵一、题目名称:风险投资 时间限制:1000ms内存限制:256M 题目描述: 风险投资是一种感性和理性并存的投资方式,风险投资人一般会对请公允的第三方评估公司对投资对象…
【离散数学】第一章 测试
1. A. 对 B. 错 正确答案:A 2. A. 对 B. 错 正确答案:B 3. A. 错 B. 对 正确答案:B 4.p↔q⇔p↔q A. 对 B. 错 正确答案:A 5. A. 对 B. 错 正确答案:A 6.n个命题变元组成的命题公式共有( )种不同的…
隐函数求导例题及解析
隐函数求导
两边同时对x求导 yy(x)yy(x)yy(x)是由方程ex−ey1cos(xy)e^x-e^y1\cos(xy)ex−ey1cos(xy)所确定的函数,求dydx\dfrac{dy}{dx}dxdy.
解: \qquad两边同时求导得: ex−eyy′−sin(xy)(yxy′)\qquad e^x-e^yy-\sin(xy)\times(…
【概率论】期末复习笔记:参数估计
参数估计目录一、点估计1. 估计量的概念2. 估计量的求法矩估计法最大似然估计法二、估计量的评选标准1. 无偏性2. 有效性3. 相合性总结三、区间估计1. 双侧区间估计2. 单侧区间估计四、正态总体参数的区间估计σ2\sigma^2σ2已知,考察μ\muμ</font>σ2\sigma…
(Week 15)综合复习(C++,字符串,数学)
文章目录T1 [Daimayuan]删删(C,字符串)输入格式输出格式样例输入样例输出数据规模解题思路T2 [Daimayuan]快快变大(C,区间DP)输入格式输出格式样例输入样例输出数据规模解题思路T3 [Daimayuan]饿饿 饭饭2&a…
[Daimayuan]新国王游戏(C++,数学)
又到了 HHH 国国庆, 国王再次邀请 nnn 位大臣来玩有奖游戏。上次国庆被众臣吐槽国王小气后,国王决定今年大方点,改变游戏规则且不再参与游戏,免得被大臣们质疑。首先, 他让每位大臣在左、 右手上面分别写下一个正整数。然后让这 nnn 位大臣排…
[Daimayuan] 算的我头都大啦(C++,数学)
爱数学的小明又回来辣!看了上次大家解决问题的方法后觉得自己实在是太笨了,同时引来了同是数学爱好者的小红的嘲笑,自尊心极强的小明气不过,便和小红打个赌,让小红出一道数学题给小明写,如果小明能在一周内…
14. 线性代数 - 线性方程组
文章目录 线性方程组矩阵行列式全排列和逆序数N阶行列式(非)齐次线性方程Hi,大家好。我是茶桁。 结束了「微积分」部分的学习之后我们稍作休整,今天正式开始另外一部分:「线性代数」的学习。小伙伴们放松完回来要开始紧张起来了。
我们之前说过,不管是哪一个工程学科,根…
L1,L2范数学习笔记
L1范数
作用:使解变为一个稀疏解,降低过拟合。
为什么会参产生稀疏解参考https://zhuanlan.zhihu.com/p/129024068 因为在0处可能是极小点(可能性受惩罚系数影响),因此容易收敛到极小点,也就是0处&#x…
简单迭代法、牛顿迭代法、Aitken加速迭代法 C++代码参考
1、简单迭代法:
参考代码:
#include<stdio.h>
#include<math.h>
#define x0 3//初值
#define MAXREPT 1000//迭代次数
#define EPS 0.5E-6//精度
#define G(x) pow(sin(x)12*x-1,1.0/3)//你的迭代函数;将原方程化为xG(x)。
int…
一本数学教材严谨和通俗哪个更重要?
一本教材也许无法同时兼顾严谨和通俗,而且在不同的场景下,严谨和通俗的重要性也不尽相同: 在正式的学术场合,严谨当然重要,一些不严谨的教材可能无法通过审校,在读者存在疑问的时候,也不一定能给…
【白话机器学习系列】白话梯度下降
白话梯度下降
梯度下降是机器学习中最常见的优化算法之一。理解它的基本实现是理解所有基于它构建的高级优化算法的基础。 文章目录 优化算法一维梯度下降均方误差梯度下降什么是均方误差单权重双权重三权重三个以上权重 矩阵求导结论 优化算法 在机器学习中,优化是…
【华为OD题库-047】求最小步数-java
题目 求从坐标零点到坐标点n的最小步数,一次只能沿横坐标轴向左或向右移动2或3. 注意:途径的坐标点可以为负数 输入描述 坐标点n 输出描述 输出从坐标零点移动到坐标点n的最小步数 备注 1< n < 10^9 示例1: 输入 4 输出 2 说明 从坐标零点移动到4,…
【动态规划】【 数学】C++算法:514自由之路
作者推荐
【动态规划】458:可怜的小猪
涉及知识点
动态规划 数学
力扣514 自由之路
电子游戏“辐射4”中,任务 “通向自由” 要求玩家到达名为 “Freedom Trail Ring” 的金属表盘,并使用表盘拼写特定关键词才能开门。 给定一个字符串 ring &#x…
关于机器学习的一些数学基础(一)
Big O notation
一般我们描述算法复杂度时,会使用大O符号。例如冒泡排序的复杂度是O(n^2),快排与归并排序的复杂度为O(nlogn)。那么什么是大O符号呢。
一般呢,我们说f(x)O(g(x)),即指f(x)与g(x)的量级差不多,使用数学…
【组合数学】全错位排列的递推公式推导
简介
假设现在我有三个信封A,B,C,并且现在有三个信纸a,b,c。 按照道理的话是,a塞入A信封,b塞入B信封,c塞入C信封。 但是现在,想要问,对于a,b&…
codeforces 1445 D Divide and Sum (组合数)
题面 题意 题解 我们举例可以发现,每种可能通过排序相减之后相加,所得到的结果都是一样的,就是序列排序后,n个大的-n个小的和那么我们现在只需要算出有多少种可能就行了,对于2n个数,每次选取n个数到一个序列…
码蹄杯语言基础:循环结构(C语言)
码蹄集网站地址:https://www.matiji.net/exam/ojquestionlist
⭐MT1185while循环
请编写一个简单程序,从小到大输出所有小于8的正整数和0(从0开始输出)。
格式 输入格式: 无
输出格式: 输出整型&#x…
Codeforces Round 877 div2 C No Prime Differences
目录 一、题目
二、题目分析
三、 一、题目
传送门
C. No Prime Differences
time limit per test
2 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
You are given integers n and m. Fill an n by m grid with the…
【复变函数笔记】傅里叶变换和拉普拉斯变换
文章目录 一、傅里叶变换和拉普拉斯变换的定义1. 傅里叶积分2. 傅里叶变换3. 单位脉冲函数和单位阶跃函数4. 拉普拉斯变换 二、常见函数的傅里叶变换和拉普拉斯变换三、傅里叶变换和拉普拉斯变换的性质 一、傅里叶变换和拉普拉斯变换的定义
1. 傅里叶积分
傅里叶积分定理 若 …
FO-like Transformation
参考文献:
[RS91] Rackoff C, Simon D R. Non-interactive zero-knowledge proof of knowledge and chosen ciphertext attack[C]//Annual international cryptology conference. Berlin, Heidelberg: Springer Berlin Heidelberg, 1991: 433-444.[BR93] Bellare M…
朴素贝叶斯之理论部分
条件概率 假设 事件AAA:你错过上学 事件BBB:你闹钟没响 P(A)P(A)P(A)或者P(B)P(B)P(B)都很小,但是P(A∣B)P(A|B)P(A∣B)就不一定小了。 P(A∣B)P(A|B)P(A∣B)表示在BBB的条件下AAA发生的概率,例子中就是你闹钟没响的情况下错过上学…
Definition of regularity in PDE theory
Regularity is one of the vague yet very useful terms to talk about a vast variety of results in a uniform way. Other examples of such words include “dynamics” in dynamical systems (I have never seen a real definition of this term but everyone uses it, an…
[Daimayuan] 全部相等(C++,数学)
* 注:题名的灵感来自 代码源 #914: 一半相等 给定长度为 n n n 的数组 A {A} A。
派派非常喜欢 所有元素出现频率相同 的数组,但这样的数组却不常有。派派很伤心 (;༎ຶД༎ຶ)。不过聪明的你,发现总能从 A {A} A 中挑选一个子序列满足上…
分圆多项式 cyclotomic polynomial
翻译自维基百科
数学上将第nnn个分圆多项式写作Φn(X)\Phi_n(X)Φn(X)。
定义为:
对于任意正整数nnn,Φn(X)\Phi_n(X)Φn(X)是一个不可约的首一多项式,满足Φn(X)∣xn−1\Phi_n(X)|x^n-1Φn(X)∣xn−1,任意k<nk<nk…
数学回味系列之9 - 绳子逃生问题
问题提出: 你被困在一幢200米高的大楼楼顶。楼顶有一个铁钩(可以挂住绳子),大楼正中间,也就是100米高的位置上,有一个可以落脚的金属支架。 你手里有一根150米长的绳子和一把刀(可切开绳子&…
数学分析:数项级数的性质
数学分析:数项级数的性质
通过上一节的内容,我们知道:级数的收敛与数列的收敛本质上是一回事。这使得通过数列的性质推导级数的性质成为了可能。
定理 1. 数项级数收敛的必要条件:设 ∑n1∞xn\sum_{n1}^{\infty}x_{n}∑n1∞xn…
函数极限:函数在一点处的极限
数学分析笔记——总目录 文章目录函数极限:函数在一点处的极限函数在点 x0x_0x0 处的极限:定义函数在点 x0x_0x0 处的极限:性质唯一性局部保序性局部保不等式性局部有界性夹逼性函数在点 x0x_0x0 处的极限:运算(线性)相加运…
数学分析:集合的基本运算
文章目录数学分析:集合的基本运算集合的并集合的交集合的差集合的补集合的运算律参考文献数学分析:集合的基本运算
集合有 并、交、差、补 四种基本运算。
集合的并
定义 1(集合的并):设 A,BA,BA,B 为两个集合&…
数列极限:数列极限的概念
文章目录数列极限的概念数列基础数列的概念特殊数列等差数列(算术数列)等比数列(几何数列)有界数列单调数列子列数列极限数列极限的定义数列极限的几何意义方式一方式二数列的敛散性分析参考文献数列极限的概念
这一节࿰…
GDKOI2016 Day2 T4 小学生数学题
T4 小学生数学题 求∑i1n1imodpk首先,我们把原式分成两部分,一部分对于p有逆元,另一部分没有。 即原式 1p∑i1⌊np⌋1i∑a1p−1∑i0⌊np⌋−11ai∗pmodpk剩余一部分,由于个数少于p,暴力做就行了。 然后分类讨论part …
【复变函数】2021-09-15-复变函数/解析函数的一些想法(五)(算不上笔记)
一、
(先吐槽个事,bing的界面做的真的是清奇无比,我看腻了任务栏在上面之后把任务栏切到了左边,结果它竟然把一部分功能挤到了屏幕之外,笔记本屏幕震怒)
复变函数的定义; 单值复变函数与多值复…
手把手入门神经网络系列(1)_从初等数学的角度初探神经网络
作者: 龙心尘&&寒小阳 时间:2015年11月。 出处: http://blog.csdn.net/longxinchen_ml/article/details/50082873 http://blog.csdn.net/han_xiaoyang/article/details/50100367 声明:版权所有,转载请联系…
UWA学堂|虚幻4渲染编程(数学篇)
本课程介绍了一些游戏开发中常用的数学原理推导,共分为五小节:
第一节从头开始复习游戏开发所需要的数学理论,然后再结合例子,把抽象的数学理论变成可以在屏幕上看到的效果和代码,一边做效果一边重新复习数学。
第二…
第1周周赛——开学第一课(题解)——出自(Codeforces Good Bye 2015 和 HDU1717)
A题:
A题题目链接
题目描述: New term and days TimeLimit:2000MS MemoryLimit:256MB64-bit integer IO format:%I64dProblem DescriptionToday is Wednesday, the third day of the week. Whats more interesting is that tomorrow is the last day…
rank(A)=rank(A^TA)
Let x∈N(A)x\in N(A)x∈N(A) where N(A)N(A)N(A) is the null space of AAA. Hence Ax0⇒ATAx0⇒x∈N(ATA)Ax0 \Rightarrow A^TAx0 \Rightarrow x\in N(A^TA)Ax0⇒ATAx0⇒x∈N(ATA)
It means that N(A)⊂N(ATA)N(A)\subset N(A^TA)N(A)⊂N(ATA). On the other hand, suppose …
Codeforces Round #341 (Div. 2)总结
A题:
A题题目链接
题目描述: A. Wet Shark and Odd and Eventime limit per test2 secondsmemory limit per test256 megabytesinputstandard inputoutputstandard outputToday, Wet Shark is given n integers. Using any of these integers no more…
用Java实现可交互的贝塞尔曲线(Bezier curve)
关于贝塞尔曲线的详细数学原理及公式可参考:
贝塞尔曲线_百度百科
我们来谈谈贝塞尔曲线 本文给出了一种用Java实现贝塞尔曲线的方法,并且可以用鼠标拖动改变锚点。
效果演示图: 这里引用百度百科给出的公式: 二次方公式 三次方…
483. 最小好进制
2021-06-18 LeetCode每日一题
链接:https://leetcode-cn.com/problems/smallest-good-base/
标签:数学、二分查找 题目 对于给定的整数 n, 如果n的k(k>2)进制数的所有数位全为1,则称 k(k>2…
HDOJ-3343 An ant's story(积分)
橡皮筋均匀伸长mm/sm \text{ m/s}m m/s,蚂蚁匀速从一端以vm/sv \text{ m/s}v m/s走向另一端,问蚂蚁何时走到终点.
变换位移的方法: 设相对位移xxx,有比值关系dxvdtLLmt\displaystyle \frac{dx}{vdt} \frac{L}{Lmt}vdtdxLmtL,解: L∫0Ldx∫0TLLmtvdtLvmln(Lmt)∣0TLvmln…
Convolution theorem in finite domain
1、https://math.stackexchange.com/questions/2305411/convolution-theorem-in-finite-domain2、https://math.stackexchange.com/questions/1866465/is-it-possible-to-use-the-convolution-theorem-on-a-finite-interval-integral-l3、https://math.stackexchange.com/quest…
PDE+图像处理-一些文献标签
1、Antil, H., & Bartels, S. (2017). Spectral Approximation of Fractional PDEs in Image Processing and Phase Field Modeling. Computational Methods in Applied Mathematics, 17(4). doi:10.1515/cmam-2017-0039
2、https://sites.oxy.edu/ron/math/300/16/comps/…
人工智能所需高等数学知识大全(收藏版)
来源:投稿 作者:愤怒的可乐 编辑:学姐 不懂数学是学不好人工智能的,本系列文章就汇总了人工智能所需的数学知识。本文是高等数学篇。 另有线代篇和概率论篇
函数与极限
函数
yf(x) ,x是函数f的自变量,y是因变量
函…
[NOIP1998 提高组] 车站
题目描述
火车从始发站(称为第 1 站)开出,在始发站上车的人数为 a,然后到达第 2 站,在第 2 站有人上、下车,但上、下车的人数相同,因此在第 2 站开出时(即在到达第 3 站之前&#x…
【洛谷P3708】koishi的数学题
题目描述
Koishi在Flandre的指导下成为了一名数学大师,她想了一道简单的数学题。
输入一个整数n,设,你需要输出。
按照套路,Koishi假装自己并不会做这道题,就来求你帮忙辣。
输入输出格式
输入格式: …
牛客寒假算法基础集训营2_H处女座的测验(一)(数学、质数、构造)
题目链接:https://ac.nowcoder.com/acm/contest/327/H
题目描述:
处女座进行了一场c语言的考试,要求很简单,输出2000个正整数,并且满足以下条件:
1.任意两个数互质
2.任意两个数x,y,满足&am…
【线性代数笔记】线性代数知识点总结、概念之间关系总结
矩阵的秩
1. 基础
初等变换不改变矩阵的秩。
阶梯形矩阵非零行的个数即为该矩阵的秩。 r ( A ) r ( A T ) r ( A T A ) r ( A A T ) r(\boldsymbol{A})r(\boldsymbol{A}^{\mathrm{T}})r(\boldsymbol{A}^{\mathrm{T}}\boldsymbol{A})r(\boldsymbol{A}\boldsymbol{A}^{\mat…
牛顿-莱布尼茨公式的运用
前置知识:牛顿-莱布尼茨公式
题1: f f f在 [ a , b ] [a,b] [a,b]上连续, F ( x ) ∫ a x ( x − t ) f ( t ) d t F(x)\int_a^x(x-t)f(t)dt F(x)∫ax(x−t)f(t)dt,求 F ′ ′ ( x ) F(x) F′′(x)
解: F ( x )…
第十四届全国大学生数学竞赛决赛(非数类)游记+答案解析
2023/5/27 20:08:今天早上9:00~12:00考了数学竞赛国赛。广州是真的热啊!西安才17度,还下着小雨,到广州之后那个艳阳直接给我人干废了,去酒店的路上步行了20分钟真的要死了已经。
拿到卷子的我是崩溃的,用正…
codeforces 1459 C Row GCD
原题链接 翻译 思路 辗转相除法的扩展性质 : gcd(x,y) gcd(x,y-x)由性质我们可以化解表达式 :gcd(a1bi,a2bi,…,anbi) gcd(a1bi,a2-a1,a3-a2,…,an-an-1)题中还有还有两大坑点,然后我就wa了两发,第一个要开long long ,第二个记得要提前先算出…
codeforces 1244 C 数论
原题链接 洛谷翻译 思路 1.由题意知道,败一场不得分,对最后的结果没有影响,所以我们可以不考虑失败的场数,只考虑胜场和平长,最后拿n减就是败场的次数 2.只需要输出一种符合题意的结果即可,我们可以这样想&…
codeforces 1228 C 数论
原题链接
Let’s introduce some definitions that will be needed later.
Let prime(x) be the set of prime divisors of x. For example, prime(140){2,5,7}, prime(169){13}.
Let g(x,p) be the maximum possible integer pk where k is an integer such that x is divi…
定积分求含无穷大的式子的和习题
前置知识:定积分求含无穷大的式子的和
习题1
计算 lim n → ∞ 1 1 3 2 1 3 ⋯ n 1 3 n 4 3 \lim\limits_{n\to\infty}\dfrac{1^{\frac 13}2^{\frac 13}\cdotsn^{\frac13}}{n^{\frac 43}} n→∞limn34131231⋯n31
解: \qquad 原式…
AcWing 每日一题 2022/5/2【2048. 干草】
AcWing 每日一题 2022/5/2【2048. 干草】
奶牛们又来捣乱了!
农夫约翰精心整理的 N 堆干草,每堆干草的高度相同。
但是,奶牛们趁着他不注意在干草堆之间移动了一些干草捆,使得各个干草堆的高度可能不再相同了。
给定所有干草堆…
AcWing 每日一题 2022/4/30【1959. 奶牛芭蕾】
AcWing 每日一题 2022/4/30【1959. 奶牛芭蕾】
为了挑战人们将奶牛视为笨拙生物的成见,农夫约翰的奶牛贝茜报名参加了芭蕾舞入门班。
她的最后一场演出是下周,约翰想帮她搭建一个足够大的长方形舞台,这样她就可以在不从舞台边沿跌落的情况下…
AcWing 每日一题 2022/4/29【1968. 奶牛赛跑】
AcWing 每日一题 2022/4/29【1968. 奶牛赛跑】
为了解决谁是跑的最快的奶牛的长期争论,贝茜和艾希决定在农场中来一场赛跑。
两头奶牛在同一时间从同一地点出发,朝同一方向奔跑。
每个奶牛的奔跑过程都可以划分为若干段。
在每一段行程中,…
求极限的若干方法经验和教训
求极限的若干方法经验和教训 文章目录求极限的若干方法经验和教训导数定义方法1.xnenlnxx^ne^{n\ln x}xnenlnx代换,常见于除式的n次方2.对数字敏感拉格朗日中值方法1.公式中的x,x0x,x_0x,x0不一定是一个数,还可以是一个函数,只要两个函数有相同的趋向就可以应用拉格朗日中值…
推荐系统中的相似度度量
推荐系统中的相似度度量 相似度计算是数据挖掘,推荐引擎中的最基本问题,例如在推荐系统(Recommender Systems,简称RSs)中计算带推荐物品(Item)相似度,或是用户(User)之间的相似度以期获得兴趣口味(Taste)相似的用户时,…
[Unity基础]游戏中的数学
一、坐标系
1.世界坐标系:使用左手坐标系,即z轴方向跟人眼向前看的方向一致(右手坐标系z轴方向跟人眼向前看的方向相反)
2.本地坐标系
3.屏幕坐标系:左下为原点,右上为屏幕宽高
4.界面坐标系:左上为原点࿰…
专升本高数学习总结——微分
基本式微分法则罗尔定理拉格朗日中值定理微分中值定理微分方程基本概念可分离变量的微分方程最简单的一阶线性微分方程二阶常系数线性微分方程 基本式
dy f’(x) • dx
y:原函数 f’(x):导函数 x:自变量 微分法则
yf(u),ug(x) yf[g(x)]的微分为 dy f’(u)du f’(u) g…
专升本高数学习总结——导数(2)
洛必达法则已知函数求某一点的斜率计算函数单调性极值计算函数凹凸性拐点 洛必达法则
在极限中使用
已知函数,求某一点的斜率
例如求某函数中的某一点的法线
计算函数单调性、极值 计算函数凹凸性、拐点 主要都是一些记忆性的东西
专升本高数学习总结——导数(1)
基本求导公式求导基本式求导运算复杂函数求导判断是否可导 基本求导公式 注意反函数三角函数应用也比较广泛,正割余割用的也比较多 求导基本式 在许多选择题填空题常见(亲身体会) 求导运算 复杂函数求导 ①式所述复杂函数即是由两个或多个初…
方向导数 directional derivative
最近在看花书,其中 4.3 中提到了方向导数 当 α0\alpha 0α0 时, ∂∂αf(xαu)uT∇xf(x)\frac{\partial}{\partial \alpha}f(\textbf{x} \alpha \textbf{u}) \textbf{u}^T \nabla_xf(\textbf{x})∂α∂f(xαu)uT∇xf(x) 是怎么得出的࿱…
卷积的本质及物理意义(全面理解卷积)
卷积的本质及物理意义 提示:对卷积的理解分为三部分讲解1)信号的角度2)数学家的理解(外行)3)与多项式的关系
1 来源 卷积其实就是为冲击函数诞生的。“冲击函数”是狄拉克为了解决一些瞬间作用的物理现象而…
高等数学(一) 微积分研究的主要对象
微积分研究的主要对象:
函数 y f(x) (a<x<b) 的变化规律 变化规律 : 微观(变化率) 宏观(变化量)
思想方法和特征
用已知来研究未知
已知是均匀变化, 在微小的局部近似把他看成均匀来研究非均匀的的问题, 但是得到的是近似值, 如果要得到精确值的话, 还需要取极限.
…
【数论知识】2:欧拉函数
欧拉函数:
在数论中,对正整数n,欧拉函数是1~n中与n互质的数的个数,记作φ(n) 。
公式: 例如:n623 则φ(n) n(1-1/2)*(1-1/3)2
证明:
利用容氏原理进行证明
从1~n中去掉p1,p2&am…
第九届“图灵杯”NEUQ-ACM程序设计竞赛个人赛 G-Num 题解
题目描述 Phenix有一个正整数N,他想知道正整数N是否可以写成a * b a b的形式(其中a > 0,b > 0) 例如3 1 ∗ 1 1 1,如果可以请输出"Yes",否则输出"No" 输入描述: 一个正整数N(0<N<2109) 输出描述: “Ye…
深度解读|数据化管理的四个层次
数据的重要性不言而喻,已经被越来越多的公司接受、熟知和应用。那么关乎数据,到底在哪些方面可以促进业务的腾飞?或者换种说法,业务对数据有哪些层次的需求?还有,数据对管理有哪些方面的贡献? 依…
codeforces 1445 C Division (质因数分解)
题面 题意 t组样例,每组给定一个p,q 找到一个最大的x,满足 p%x0 && x%q !0 题解 对于p%q ! 0 那么 x 最大就是 p对于p%q 0 ,我们就可以将 xp 变小,来满足条件,因为要满足条件1,所以x变小的只能是p的…
叉积方法,求点与线段的相对位置
叉积可以用来判断一个点在一条线段的哪个方向。 线段两个端点坐标为 A(x1, y1), B(x2, y2), 假设点 P 的坐标为 (px, py), 则向量 AP 和 BP 的坐标表示为: AP (px - x1, py - y1) BP (x2 - px, y2 - py) 叉积的计算公式为: (py…
18. 线性代数 - 线性变换
文章目录 线性空间线性变换线性变换的几何意义特征值与特征向量NumPy的矩阵操作Hi, 你好。我是茶桁。
经历了几节线性代数课程之后,终于咱们到了最后一节课了。本节课的内容说多不多,说少也不少。
我们先是要理解一下线性空间和线性变换,并且探讨一下线性变换的几何意义。…
LeetCode 2582. 递枕头:清晰的话讲述 O(1)的时间算法
【LetMeFly】2582.递枕头:清晰的话讲述 O(1)的时间算法
力扣题目链接:https://leetcode.cn/problems/pass-the-pillow/
n 个人站成一排,按从 1 到 n 编号。
最初,排在队首的第一个人拿着一个枕头。每秒钟,拿着枕头的…
pytorch_神经网络构建2(数学原理)
文章目录 深层神经网络多分类深层网络反向传播算法优化算法动量算法Adam 算法 深层神经网络
分类基础理论: 交叉熵是信息论中用来衡量两个分布相似性的一种量化方式 之前讲述二分类的loss函数时我们使用公式-(y*log(y_)(1-y)*log(1-y_)进行概率计算 y表示真实值,y_表示预测值 …
LeetCode 2578. 最小和分割:贪心(数学)
【LetMeFly】2578.最小和分割:贪心(数学)
力扣题目链接:https://leetcode.cn/problems/split-with-minimum-sum/
给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足:
num1…
Chimera:混合的 RLWE-FHE 方案
参考文献:
[HS14] S. Halevi and V. Shoup. Algorithms in HElib. In Advances in Cryptology–CRYPTO 2014, pages 554–571. Springer, 2014.[HS15] S. Halevi and V. Shoup. Bootstrapping for HElib. In Advances in Cryptology–EUROCRYPT 2015, pages 641–6…
安装 GMP、NTL、CTMalloc ,编译 OpenFHE
参考文献:
[ABB22] Al Badawi A, Bates J, Bergamaschi F, et al. Openfhe: Open-source fully homomorphic encryption library[C]//Proceedings of the 10th Workshop on Encrypted Computing & Applied Homomorphic Cryptography. 2022: 53-63.openfheorg/o…
傅立叶级数的意义--傅立叶级数是怎么来的
写这篇文章的起因是14年有道题目: 本题实质上是考察傅立叶级数的意义,因此要求扩大为不能只拘泥于傅里叶级数的计算相关问题,故作此篇。
一、课本上的内容
傅立叶级数: 设函数 f ( x ) f(x) f(x)是周期为 2 l 2l 2l的周期函数&…
3.1每日一题(定积分求压力问题)
公式: (1) 压力等于压强乘以面积 (2) 压强等于ρgh(即密度,重力加速度,水的深度)
注:题目表面不一样,实际的原理都一样,做透一道题等于做懂一类题
3.13每日一题(分部积分求不定积分)
关键在于看出两类不同类型函数的乘积,要把三角和对数以外的凑到dx上,然后分部积分
注: arctan根号x 的求导为复合求导 根号x分之一的原函数为2*根号x
3.22每日一题(二重积分求平面区域面积)
先复习求平面积分的公式 注:面对平面积分直接使用二重积分对1求积分即可;所以只需要背二重积分的两个公式: 1、直角坐标下对1积分 2、极坐标下对1积分 xy-1是等轴双曲线!!
1、先画图定区域
2、选择先对x积分还是先对…
3.26每日一题(线性非齐次的特解如何设)
1、非齐次方程有e的2x次幂:特解也有e的2x次幂
2、e的2x次幂前面有特殊的一元方程:特解要设为一般的特征方程(axb)
3、求线性齐次特征方程的特征根;
4、判断e的 rx 次幂中的 r 和特征根有没有重合的个数:…
3.27每日一题(常系数线性非齐次方程的特解)
常系数非齐次线性方程的特解如何假设(两种)形式:
1、题目中 e 的 x 次幂以及 1,都是第一种:1可以看成为e的0次幂
注:题目给的多项式是特殊的形式,我们要设为一般的形式的多项式
2、题目中sin…
[LeetCode][400]第 N 位数字
题目
400. 第 N 位数字 给你一个整数 n ,请你在无限的整数序列 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, …] 中找出并返回第 n 位上的数字。 示例 1: 输入:n 3 输出:3 示例 2: 输入:n 11 输出:…
和机器学习和计算机视觉相关的数学(from LinDahua)
From: http://dahua.spaces.live.com/default.aspx1. 线性代数 (Linear Algebra):我想国内的大学生都会学过这门课程,但是,未必每一位老师都能贯彻它的精要。这门学科对于Learning是必备的基础,对它的透彻掌握是必不可少的。我在科…
LeetCode 第391场周赛个人题解
目录 哈沙德数
原题链接
思路分析
AC代码
换水问题 II
原题链接
思路分析
AC代码
交替子数组计数
原题链接
思路分析
AC代码
最小化曼哈顿距离
原题链接
思路分析
AC代码 哈沙德数
原题链接 思路分析
签到题,不说了
AC代码
class Solution:def s…
C++二分查找算法:最大为 N 的数字组合
涉及知识点
二分查找 数学
题目
给定一个按 非递减顺序 排列的数字数组 digits 。你可以用任意次数 digits[i] 来写的数字。例如,如果 digits [‘1’,‘3’,‘5’],我们可以写数字,如 ‘13’, ‘551’, 和 ‘1351315’。 返回 可以生成的…
【面试经典150 | 数学】加一
文章目录 写在前面Tag题目来源解题思路方法一:加一 其他语言python3 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结…
C++单调向量算法:132 模式解法三枚举1
本题不同解法
包括题目及代码C二分查找算法:132 模式解法一枚举3C二分查找算法:132 模式解法二枚举2代码最简洁C二分查找算法:132 模式解法三枚举1性能最佳C单调向量算法:132 模式解法三枚举1
分析
时间复杂度
2轮循环时间复杂…
【面试经典150 | 算术平方根】
文章目录 写在前面Tag题目来源解题思路方法一:数学表达式方法二:二分法 其他语言python3 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并…
4.22每日一题(累次积分的计算:交换次序)
注:因为 是积不出的函数,所以先不用算,最后发现,出现dx与dy可以相互抵消,即可算出答案
4.28每日一题(二重积分比较大小:被积函数的大小、正负性、积分区间奇偶性)
一般比较大小的题目我们不需要把结果全部计算出来 ,而是通过奇偶性或者被积函数的大小或大于0、等于0、小于0等方法判断比较
【HUST】代数学|理想的分解习题
以下内容中,背景知识部分尽数由GPT生成,生成的方式是直接对问题进行提问,存在错误的小节我已经标注,不保证不存在其他错误。
习题部分是GPT生成后,我将看不懂的地方自己重写了一遍的结果。不保证完全正确,…
Python贝叶斯推理和概率规划
贝叶斯和概率规划
贝叶斯策略在以下情况下特别有用:
您对未知模型参数或有关数据生成的明确信息有先验信念 - 即您想要合并的有用信息。运行学习算法后,我们对参数有了更新的信念——即参数的新分布。您想要捕获结果的不确定性(模型的确定性…
读算法霸权笔记03_操控与恐吓
1. 市场失灵
1.1. 探索市场失灵现象就像寻宝游戏,很有意思
1.2. 建立一种算法来预测这个循环出现差错——多找回的两枚硬币——的可能性并对此下注
1.2.1. 盈利模式消失了,或者市场中的其他人也了解了这个模式,先行者优势消失
1.3. 在很多…
C++实现定积分运算
文章目录 题目代码 题目 代码
#include <iostream>
#include <cmath>
#include <functional>using namespace std;// 定积分函数
double integrate(function<double(double)> func, double a, double b, int num_intervals) {double h (b - a) / num…
不同像平面坐标系下的Brown畸变系数互转
不同像平面坐标系下Brown畸变系数转换
记 u , v u,v u,v为像素为单位的坐标,f为焦距,单位也是像素。
记 x , y x,y x,y为理想坐标。本文推导两种情况下的Brown畸变系数转换关系:
相同坐标系定义、不同的坐标单位(像素坐标与归一…
AcWing算法提高课-5.5.2最大公约数
宣传一下 算法提高课整理
CSDN个人主页:更好的阅读体验 原题链接
题目描述
给定整数 N N N,求 1 ≤ x , y ≤ N 1 \le x,y \le N 1≤x,y≤N 且 gcd ( x , y ) \gcd(x,y) gcd(x,y) 为素数的数对 ( x , y ) (x,y) (x,y) 有多少对。
输入格式
输…
优美的数学,形象的理解:点乘和叉乘运算如何理解
欢迎进入向量数学的核心之旅!在处理向量时,最引人入胜的两个操作是点积和叉积。虽然它们起初可能看起来很神秘,但直观地理解它们可以开启从物理学到计算机图形学等领域的丰富理解。
点积:投影阴影
点积通常被视为一个向量在另一…
Leetcode刷题224. 基本计算器
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。 示例 1:
输入:s "1 1"
输出:2示例 2:
输…
【变分法】【书籍阅读笔记】Calculus of Variation by gelfand 第一章 总结与习题题解 【更新中】
文章目录 前言1 第一章 变分法基础1.1 泛函 与 一些简单的变分问题1.2 Function Spaces/ 赋范线性空间1.3 泛函的变分: 具有极值的必要条件1. 重要引理/线性泛函的等零条件2. 泛函变分 1.4 最简单的变分问题:欧拉方程1. 欧拉方程2. 证明/欧拉方程的得出3. 欧拉方程的…
23. 图论 - 图的由来和构成
文章目录 图的由来图的构成Hi, 你好。我是茶桁。
从第一节课上到现在,我基本上把和人工智能相关的一些数学知识都教给大家了,终于来到我们人工智能数学的最后一个部分了,让我们从今天开始进入「图论」。
图论其实是一个比较有趣的领域,因为微积分其实更多的是对应连续型的…
【数学】完全剩余系与费马小定理
完全剩余系
我们定义 a i ( 1 ≤ i ≤ n ) a_i(1\le i\le n) ai(1≤i≤n) 为模 m m m 的完全剩余系当且仅当对于 1 ≤ i , j ≤ n 1\le i,j\le n 1≤i,j≤n 且 i ≠ j i\ne j ij,满足 a i ≢ a j ( m o d m ) a_i\not\equiv a_j\pmod m ai≡aj(mo…
AcWing算法提高课-5.6.1同余方程
宣传一下 算法提高课整理
CSDN个人主页:更好的阅读体验 原题链接
题目描述
求关于 x x x 的同余方程 a x ≡ 1 ( m o d b ) ax ≡ 1 \pmod b ax≡1(modb) 的最小正整数解。
输入格式
输入只有一行,包含两个正整数 a , b a,b a,b,用一…
2.证明 非单一点 Oct.2023
目录 原题解引申出的编程问题非单一点题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 提示 题解题目正解 原题
已知等边 Δ P 0 P 1 P 2 \Delta P_0P_1P_2 ΔP0P1P2,它的外接圆是 O O O,设 O O O的半径是 R R R。同时,设 Δ …
Dirac delta function (狄拉克 delta 函数)
啥意思呢?其不是一个具体的函数,而是具有某一性质的函数的总称。比如正态分布只是一个总称,不告诉均值和方差你根本不知道它长什么样。
满足什么性质呢?总结就是,该函数满足积分为1,积分区间为无穷小&…
3.6每日一题(线性方程求通解)
1、判断类型选择方法:发现以y为未知函数,以x为自变量,不符合我们学过的类型
2、此时有两种方法: (1)x 与 y 对调,此时 x 为未知函数,y 为自变量 (2)变量代换…
(统计用词)Identifiability可识别性
A researcher can meaningfully discuss the model mathematical properties, estimation of parameters, hypotheses testing about parameters only if the model is said to be identifiable。
这里的model你可理解为就是一个分布,比如正态分布,其有…
【动态规划】【数学】【C++算法】1449. 数位成本和为目标值的最大数字
作者推荐
【深度优先搜索】【树】【图论】2973. 树中每个节点放置的金币数目
本文涉及知识点
动态规划汇总
LeetCode1449. 数位成本和为目标值的最大数字
给你一个整数数组 cost 和一个整数 target 。请你返回满足如下规则可以得到的 最大 整数: 给当前结果添加…
进制转换(二进制、八进制、十进制、十六进制)
目录 一:十进制转换为二进制、八进制、十六进制
(1)整数转换
(2)小数转换
1)十进制转二进制
2)十进制转八进制
3)十进制转十六进制
二:二进制、八进制、十六进制转…
第 368 场 LeetCode 周赛题解
A 元素和最小的山形三元组 I 前后缀操作:求出前后缀上的最小值数组,然后枚举 j j j class Solution {
public:int minimumSum(vector<int> &nums) {int n nums.size();vector<int> l(n), r(n);//l[i]min{nums[0],...,nums[i]}, r[i]mi…
【数学】【记忆化搜索 】【动态规划】964. 表示数字的最少运算符
作者推荐
【动态规划】【字符串】【表达式】2019. 解出数学表达式的学生分数
本文涉及知识点
动态规划汇总 数学 记忆化搜索
LeetCoce964表示数字的最少运算符
给定一个正整数 x,我们将会写出一个形如 x (op1) x (op2) x (op3) x … 的表达式,其中每…
C++一维数组练习oj(3)
为什么C的一维数组练习要出要做那么多的题目?因为我们是竞赛学生!想要将每个知识点灵活运用的话就必须刷大量的题目来锻炼思维。
我使用的是jsswoj.com这个刷题网站,当然要钱...
C一维数组练习oj(2)-CSDN博客这是上一次的题目讲解 这道题有…
C++和Python计算金融数学方程算法模型
要点 C代码蒙特卡罗模拟金融产品估值,开发C并行计算模拟库。 算法伴随微分计算图及C代码实现释义:C应用经典的复合模式构建有向无环图,遍历有向无环图节点C实现,C使用懒惰评估计算次序,遍历代码实现,C代码…
高中数学:抽象函数难点突破(拔高)
例题1 只证明前3个小题,4,5比较简单,不给与证明 这里,第3小题,难度最高
例题2 证明单调性的方法: 1、观察图像法:前提有具体解析式,且能画出图像 2、导数法:高三才学,且…
[LeetCode][233]数字 1 的个数
题目
233. 数字 1 的个数 给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。 示例 1: 输入:n 13 输出:6 示例 2: 输入:n 0 输出:0 提示: 0 < n < 10^9 解…
【LeetCode: 面试题 16.05. 阶乘尾数 + 阶乘】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…
Leetcode—60. 排列序列【困难】
2024每日刷题(113)
Leetcode—60. 排列序列 算法思想 实现代码
class Solution {
public:string getPermutation(int n, int k) {vector<int> nums(n);// f[i] i!vector<int> f(n 1, 1); string ans;iota(nums.begin(), nums.end(), 1…
2024魔术刘谦数学魔术解密!经典的约瑟夫环问题+良好的舞台节奏
约瑟夫环
这个魔术的核心其实就是经典的约瑟夫环问题!! 考虑最简单的情况。 假设牌是2张,编号分别是1 2 会把1放到后面,扔掉2。剩下的就是最开始放在最上边的那张1。 稍微复杂一点的情况,牌的张数是2的n次方。 比如牌…
张宇2025基础三十讲高等数学笔记(数二)
本次主要是根据书课包视频的进程,第1讲的01和02,分为基础知识和书上的例题加上经典1000题对应的相关的知识点
1.基础知识
1)函数 2)反函数 3)复合函数 2.书上例题1000题
1)函数 2)反函数 3&a…
(undone) 如何计算 Hessian Matrix 海森矩阵 海塞矩阵
参考视频1:https://www.bilibili.com/video/BV1H64y1T7zQ/?spm_id_from333.337.search-card.all.click
参考视频2(正定矩阵):https://www.bilibili.com/video/BV1Ag411M76G/?spm_id_from333.337.search-card.all.click&vd_…
Codeforces Round 929 (Div. 3)(A,B,C,D,E,F,G)
这场没考什么算法,比较水,难度也不是很高。比赛链接
硬要说的话E有个 前缀和 加 二分,F是数学BFS,G是个构造 A. Turtle Puzzle: Rearrange and Negate
题意:
给你一个由 n n n 个整数组成的数组 a a a 。您必须对…
【数学】【计算几何】1453. 圆形靶内的最大飞镖数量
作者推荐
视频算法专题
本文涉及知识点
数学 计算几何
LeetCoce:1453. 圆形靶内的最大飞镖数量
Alice 向一面非常大的墙上掷出 n 支飞镖。给你一个数组 darts ,其中 darts[i] [xi, yi] 表示 Alice 掷出的第 i 支飞镖落在墙上的位置。 Bob 知道墙上所有 n 支飞…
【数学】【数论】【最大公约数】1819. 序列中不同最大公约数的数目
作者推荐
视频算法专题
本博文涉及知识点
数学 数论
LeetCode1819. 序列中不同最大公约数的数目
给你一个由正整数组成的数组 nums 。 数字序列的 最大公约数 定义为序列中所有整数的共有约数中的最大整数。 例如,序列 [4,6,16] 的最大公约数是 2 。 数组的一个…


















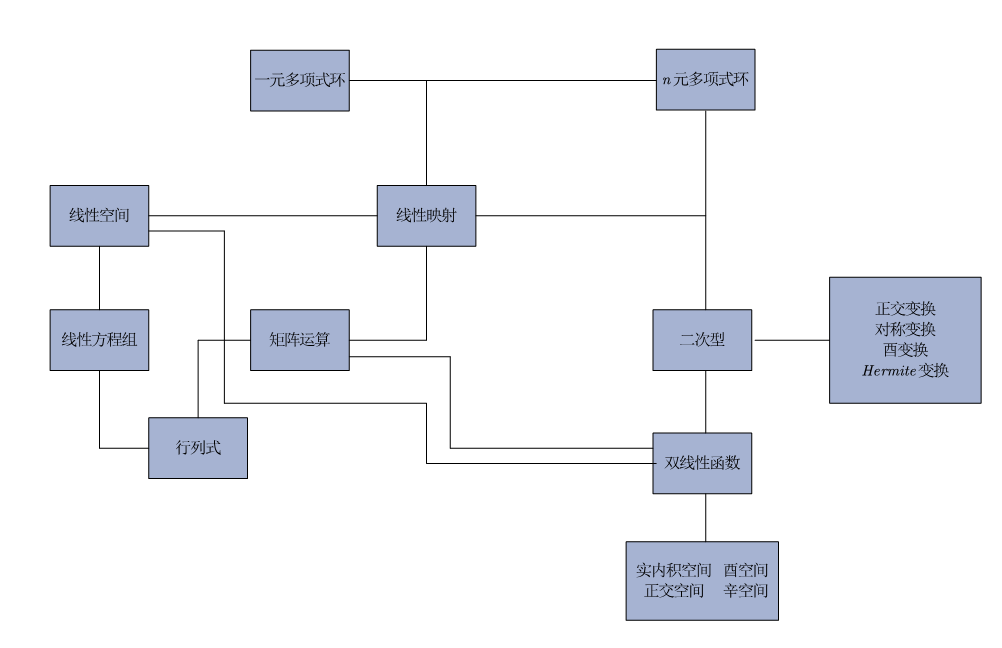

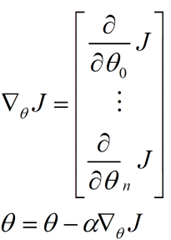





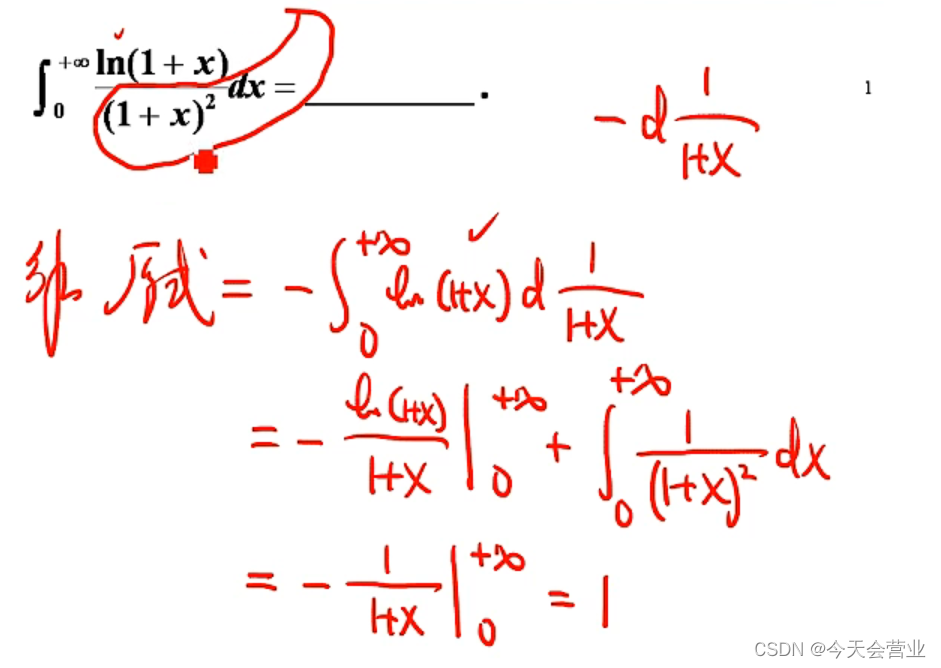
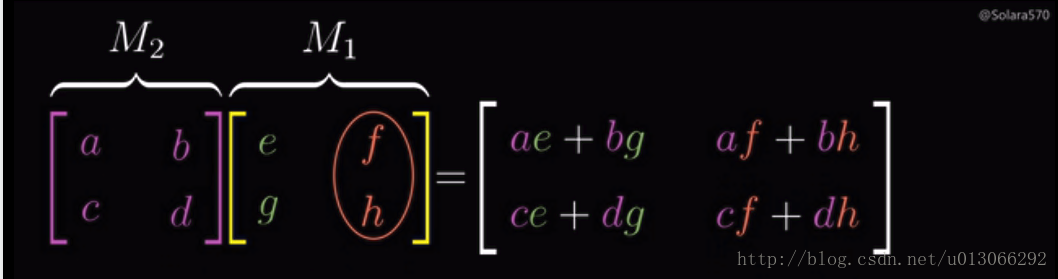






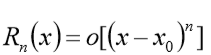










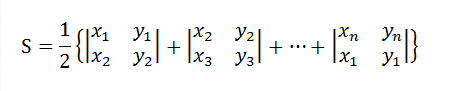


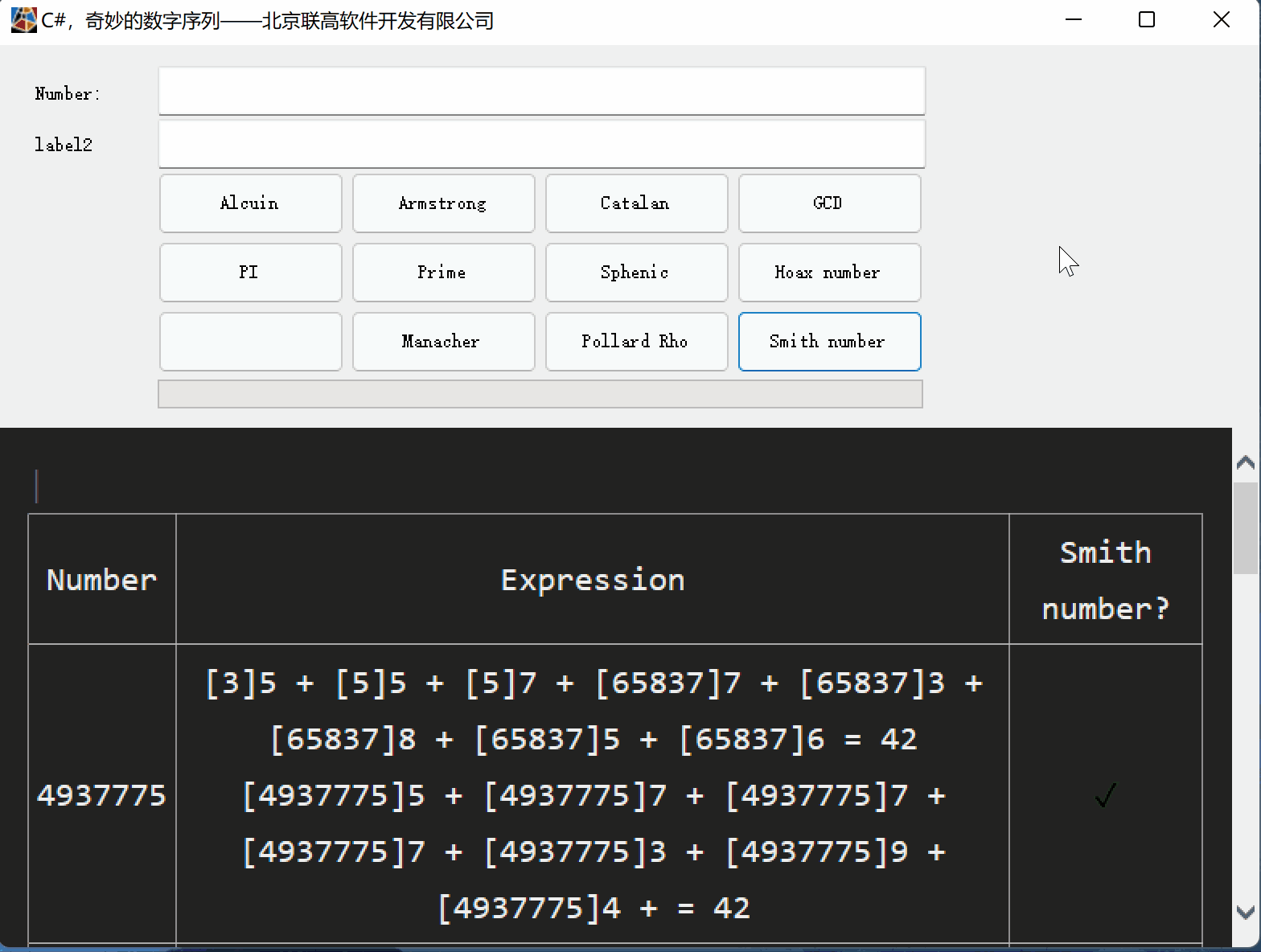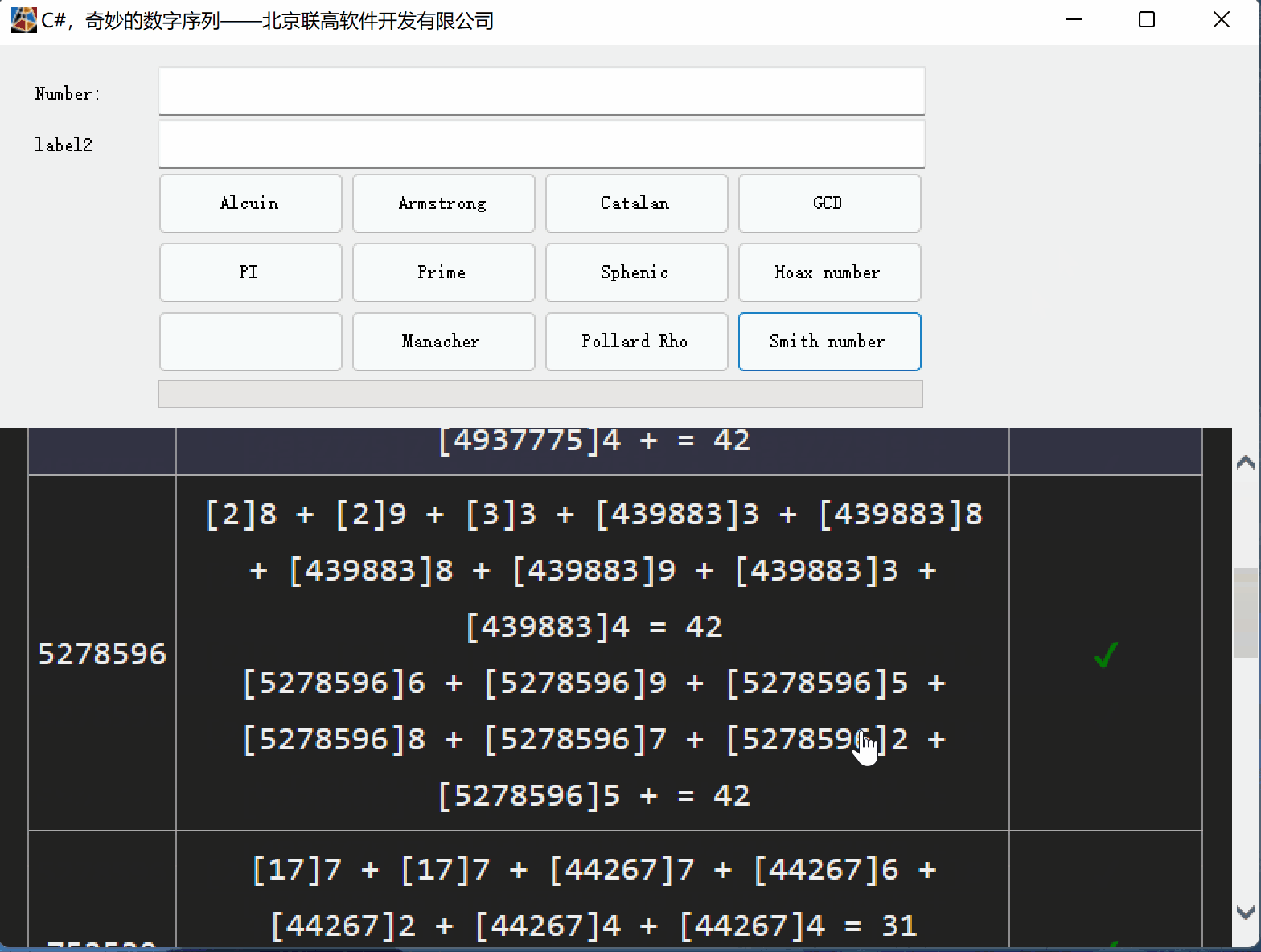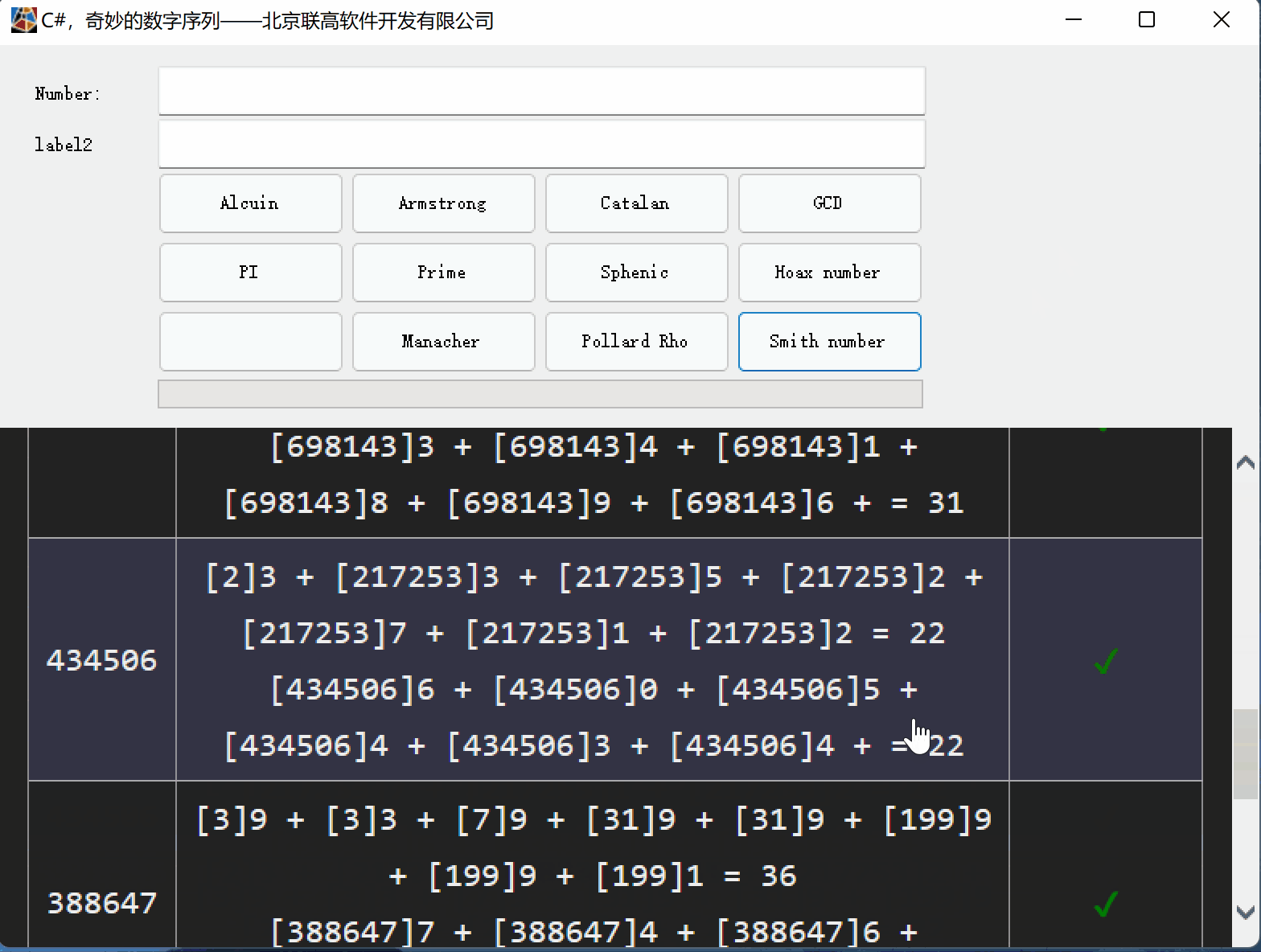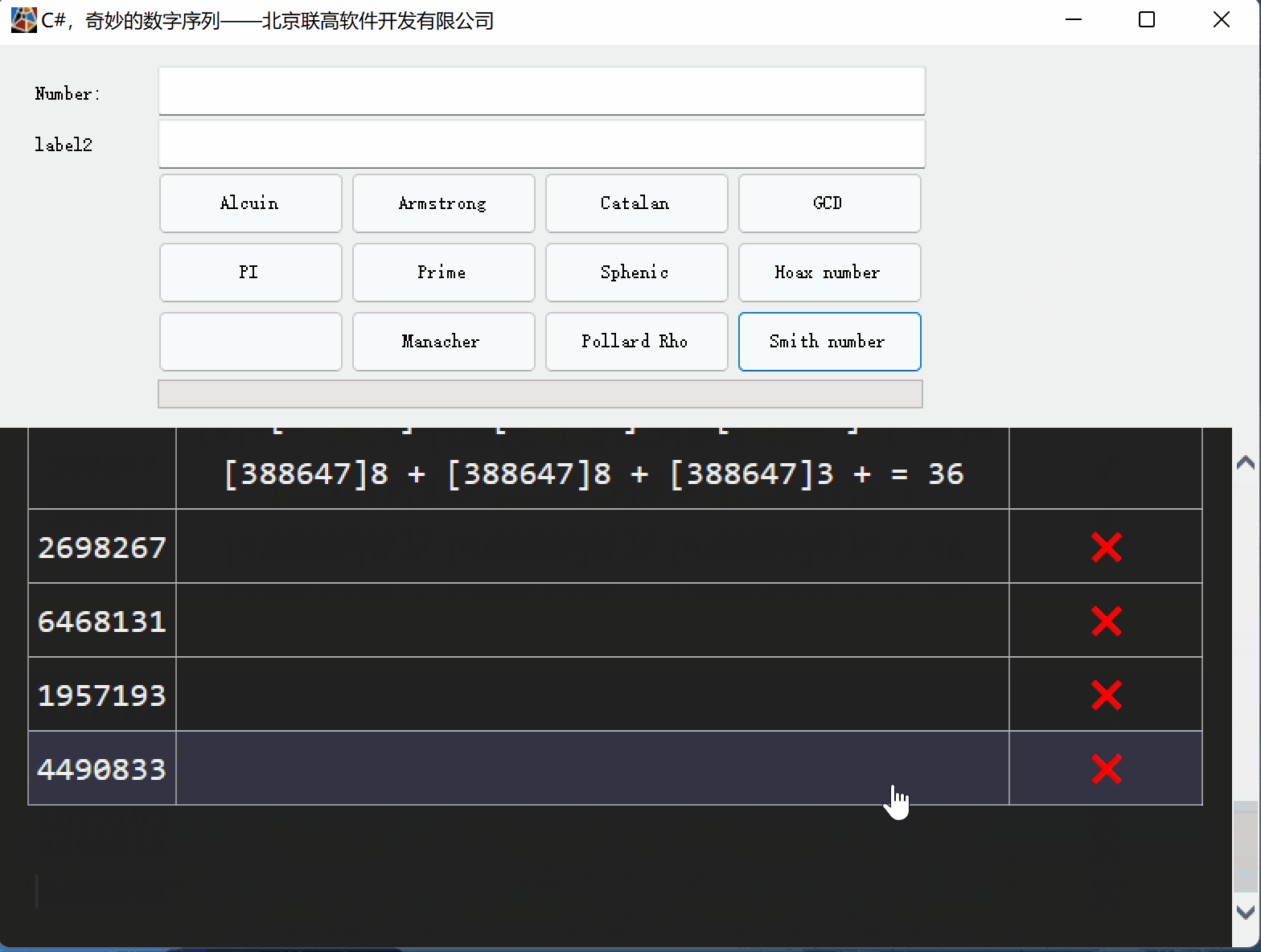










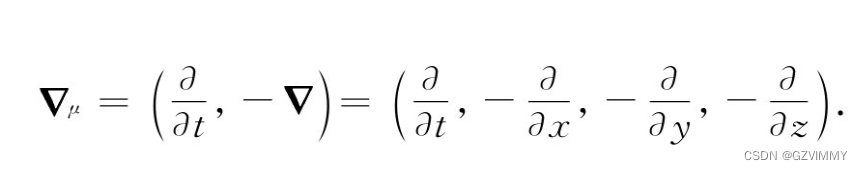










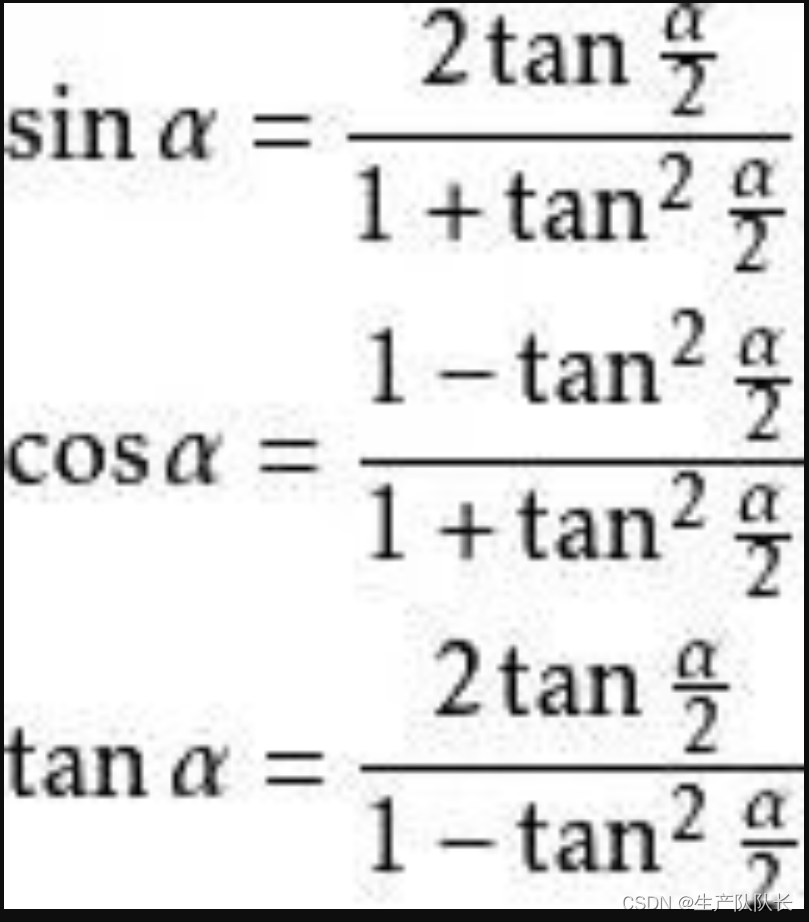

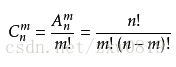







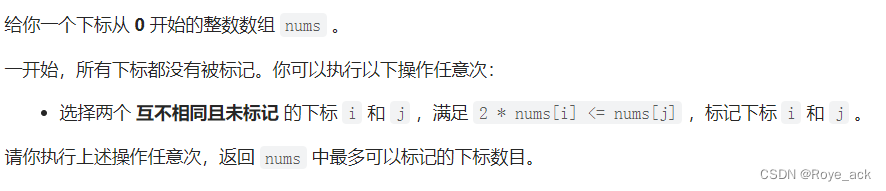

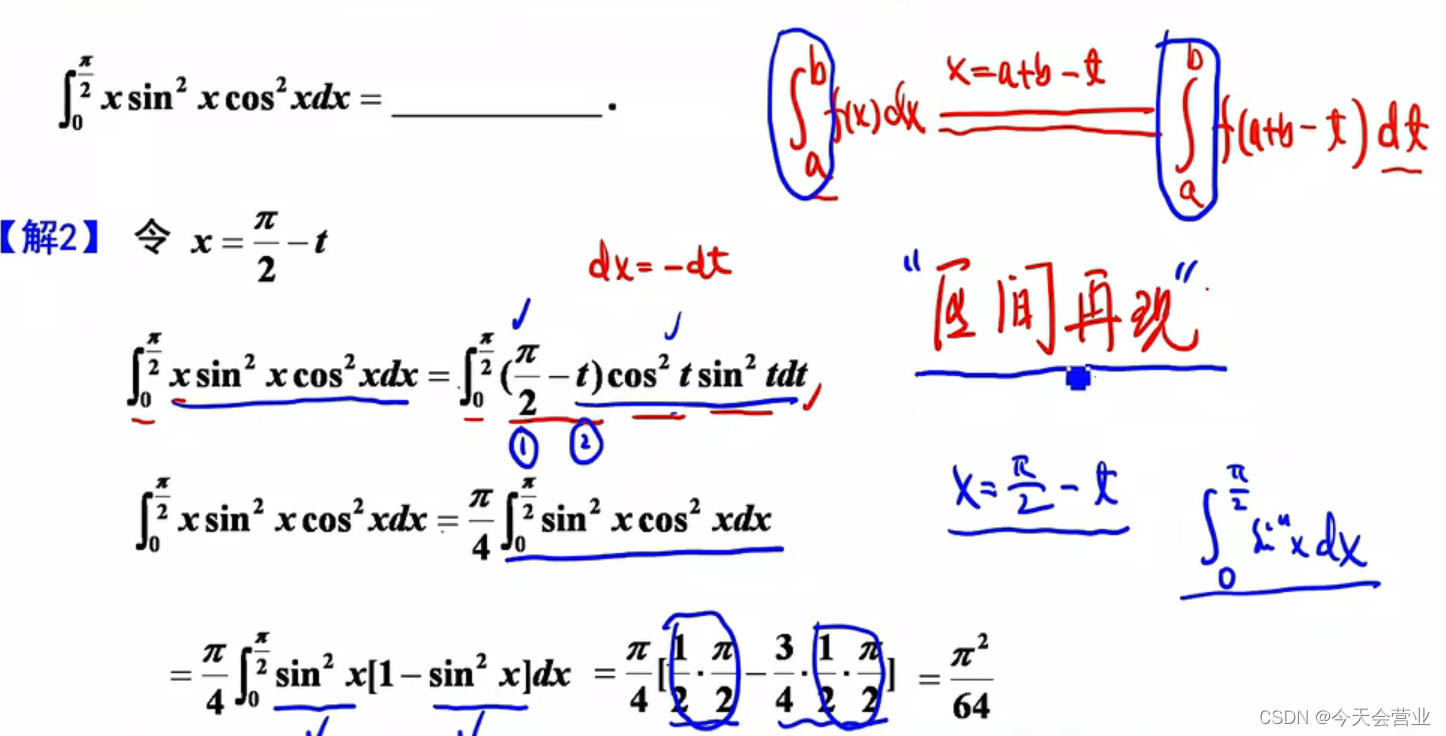




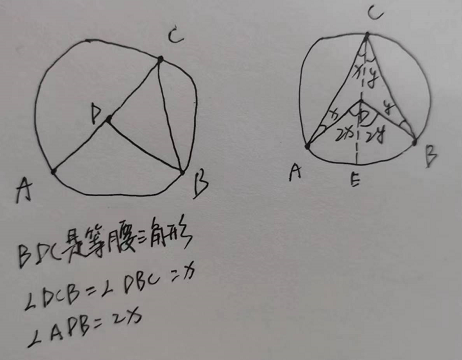


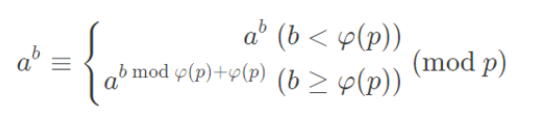



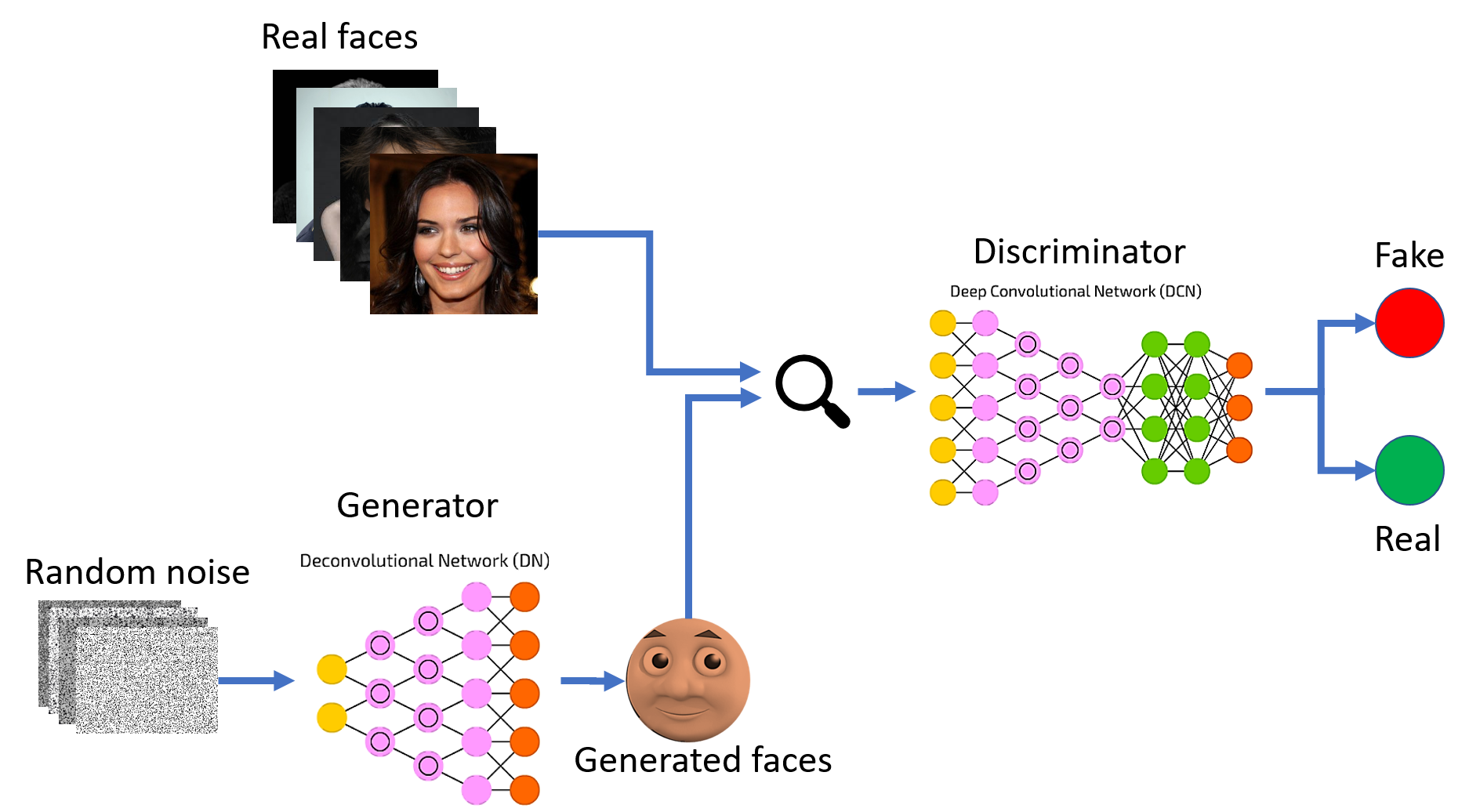



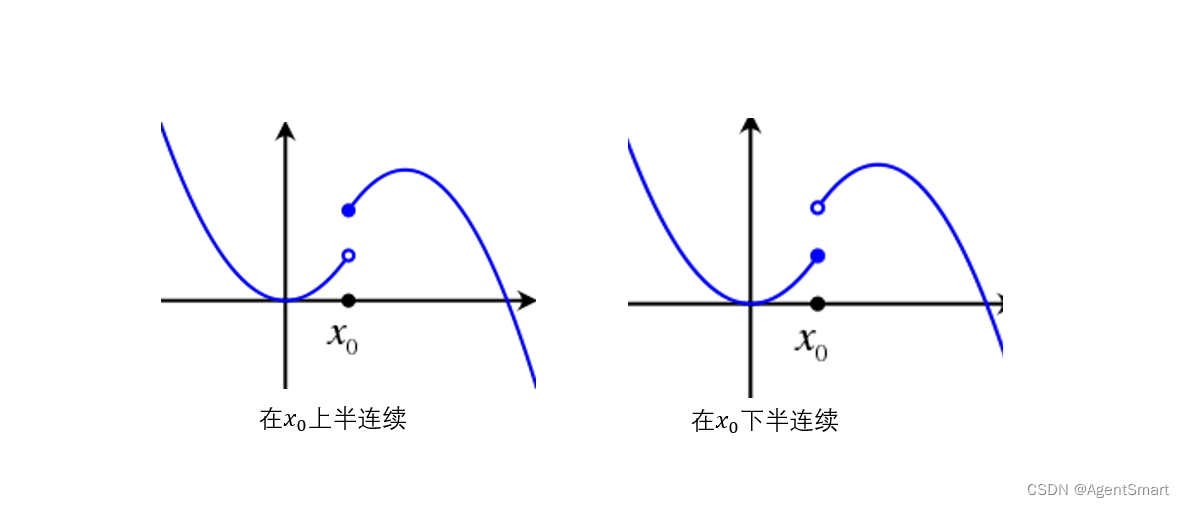








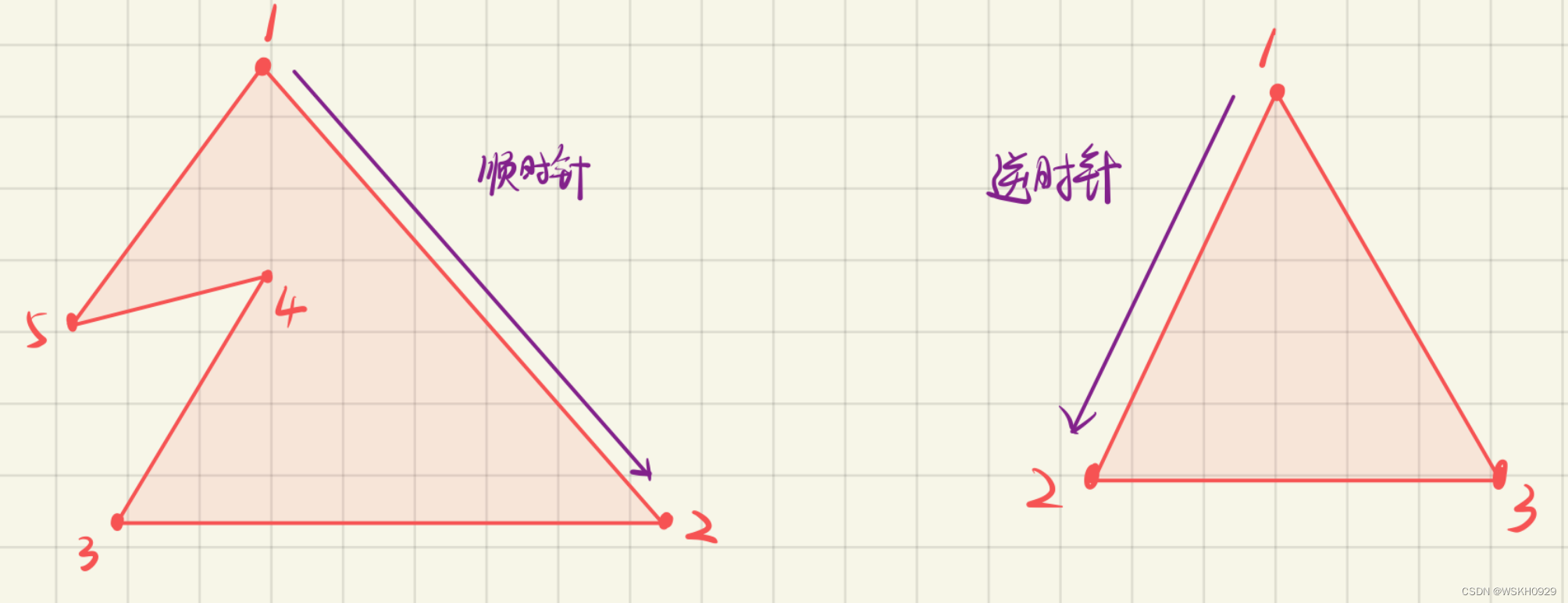





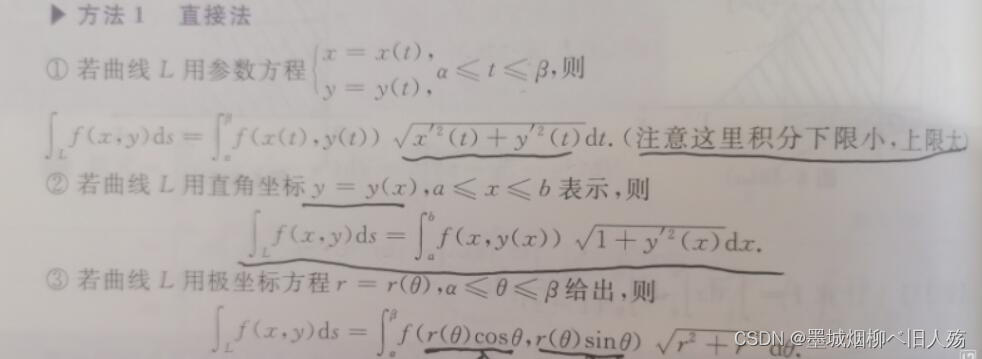



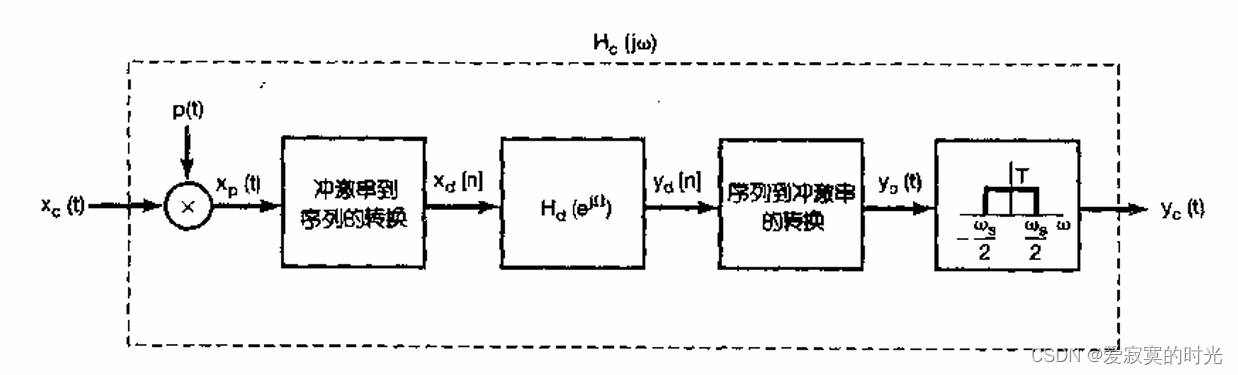



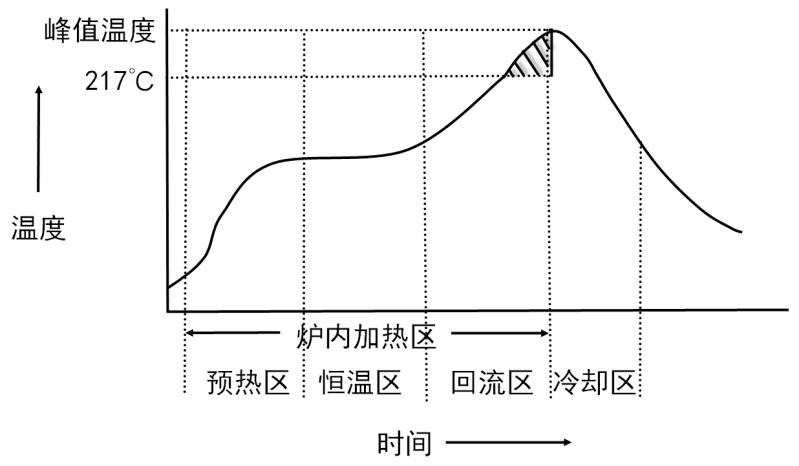






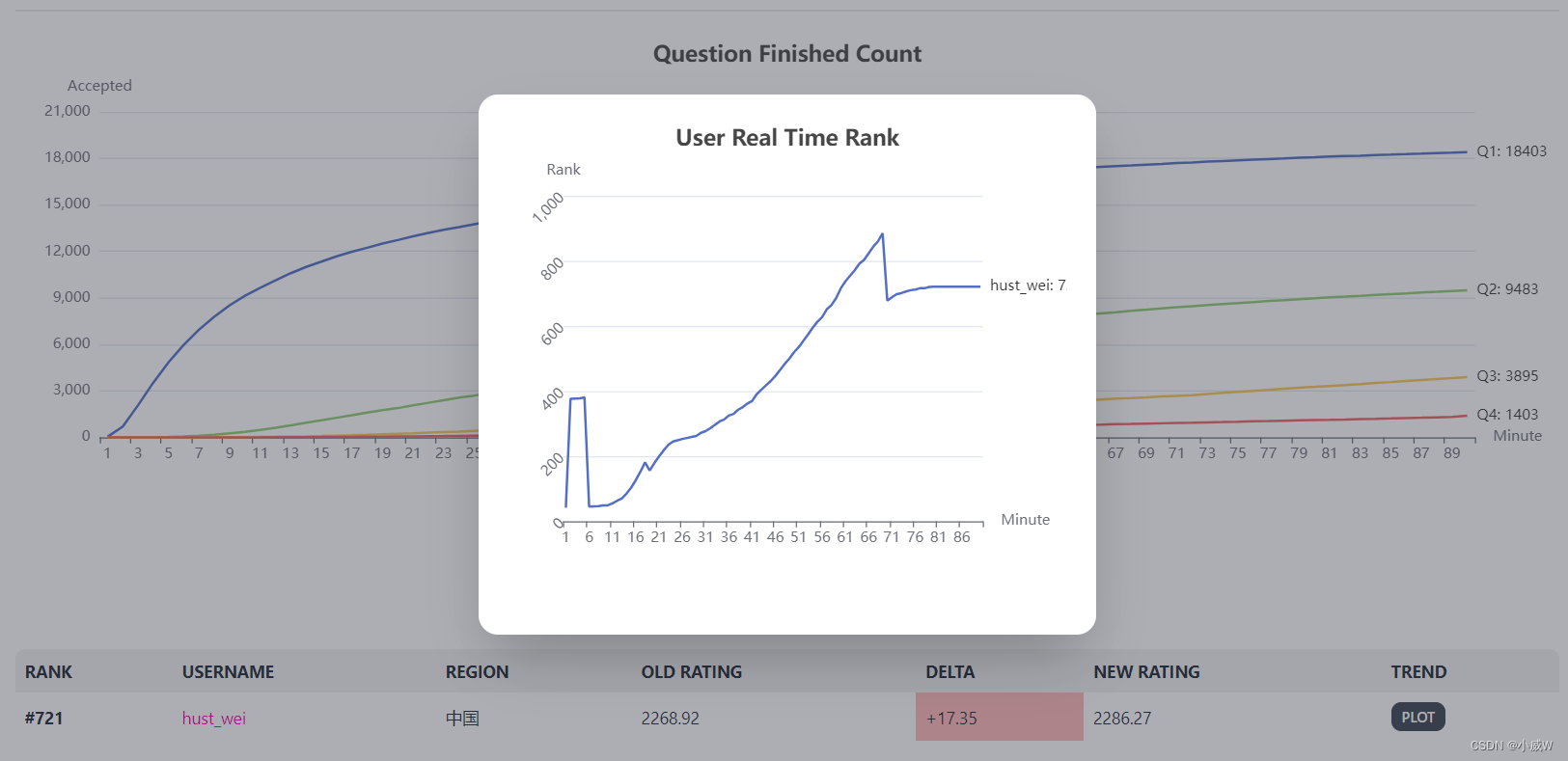
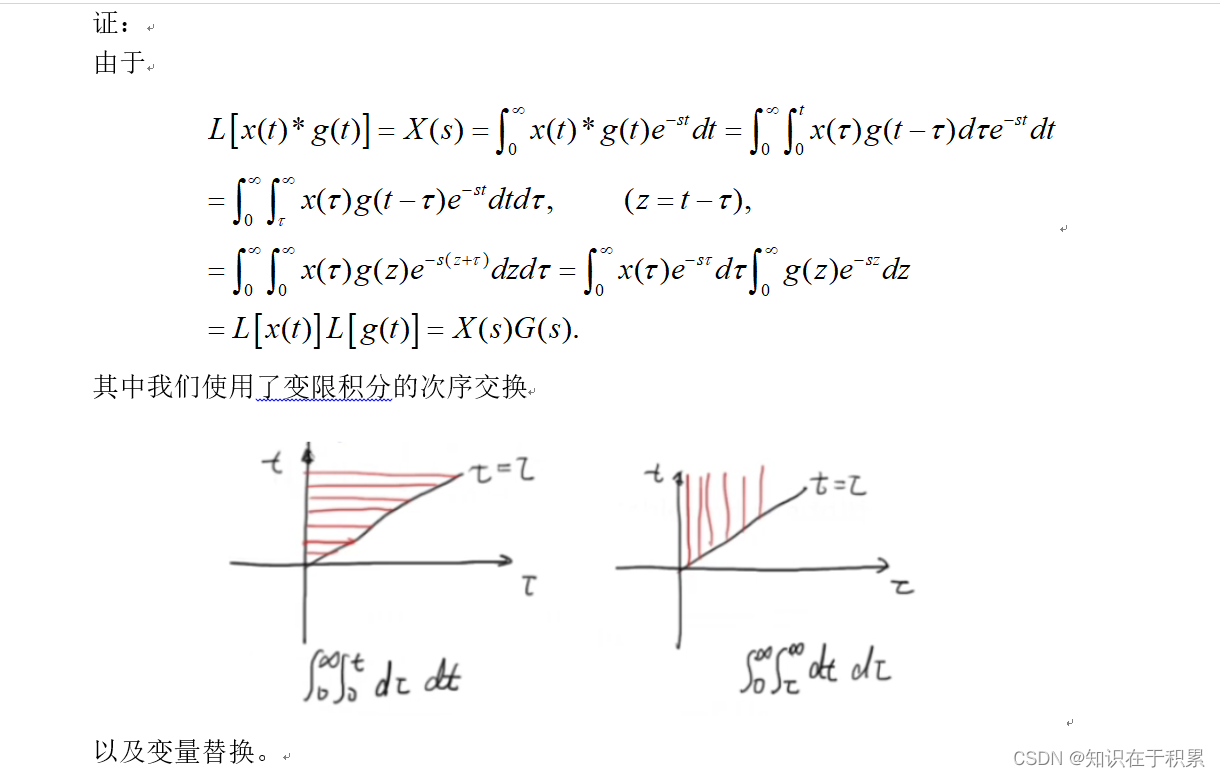

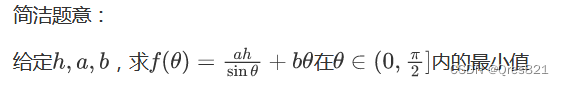








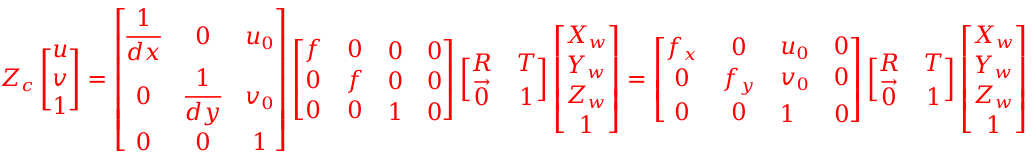
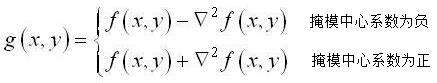
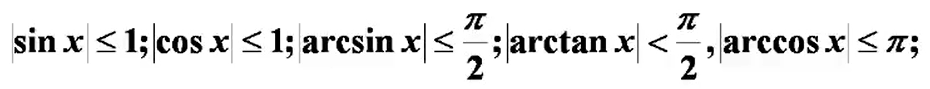
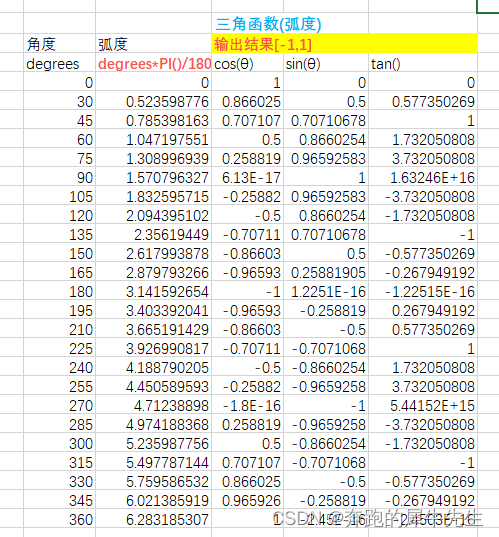
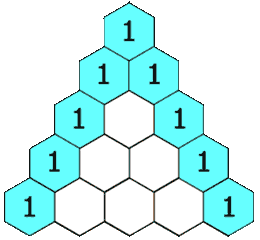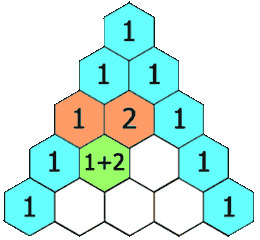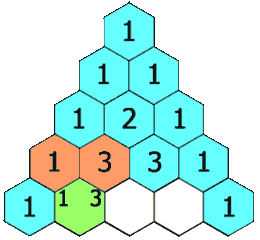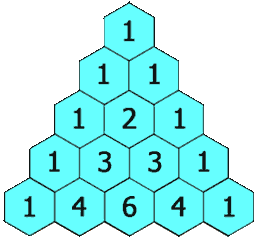

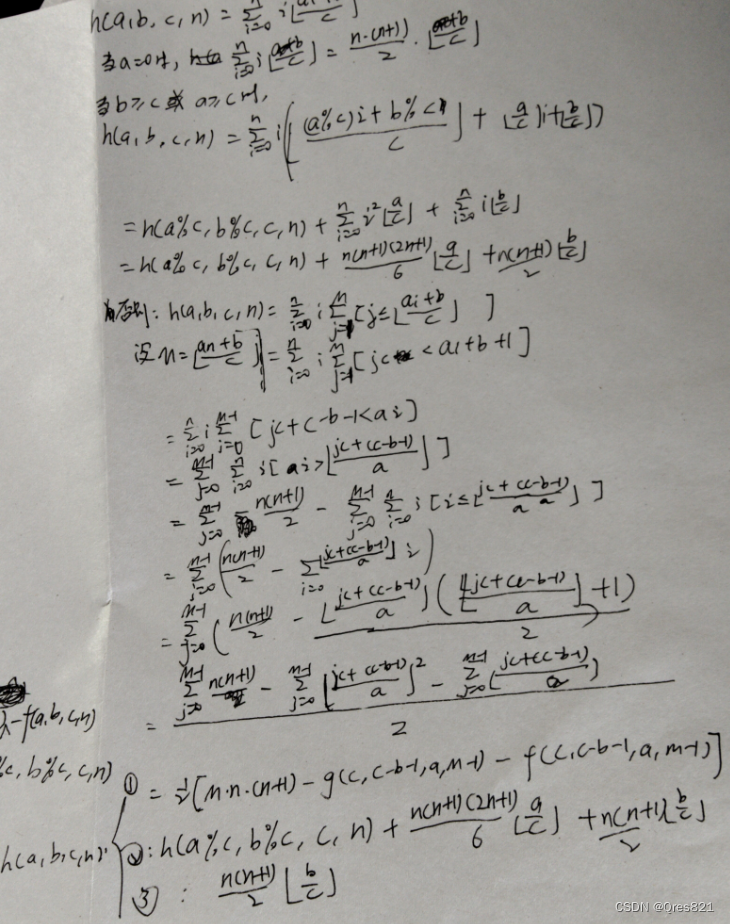






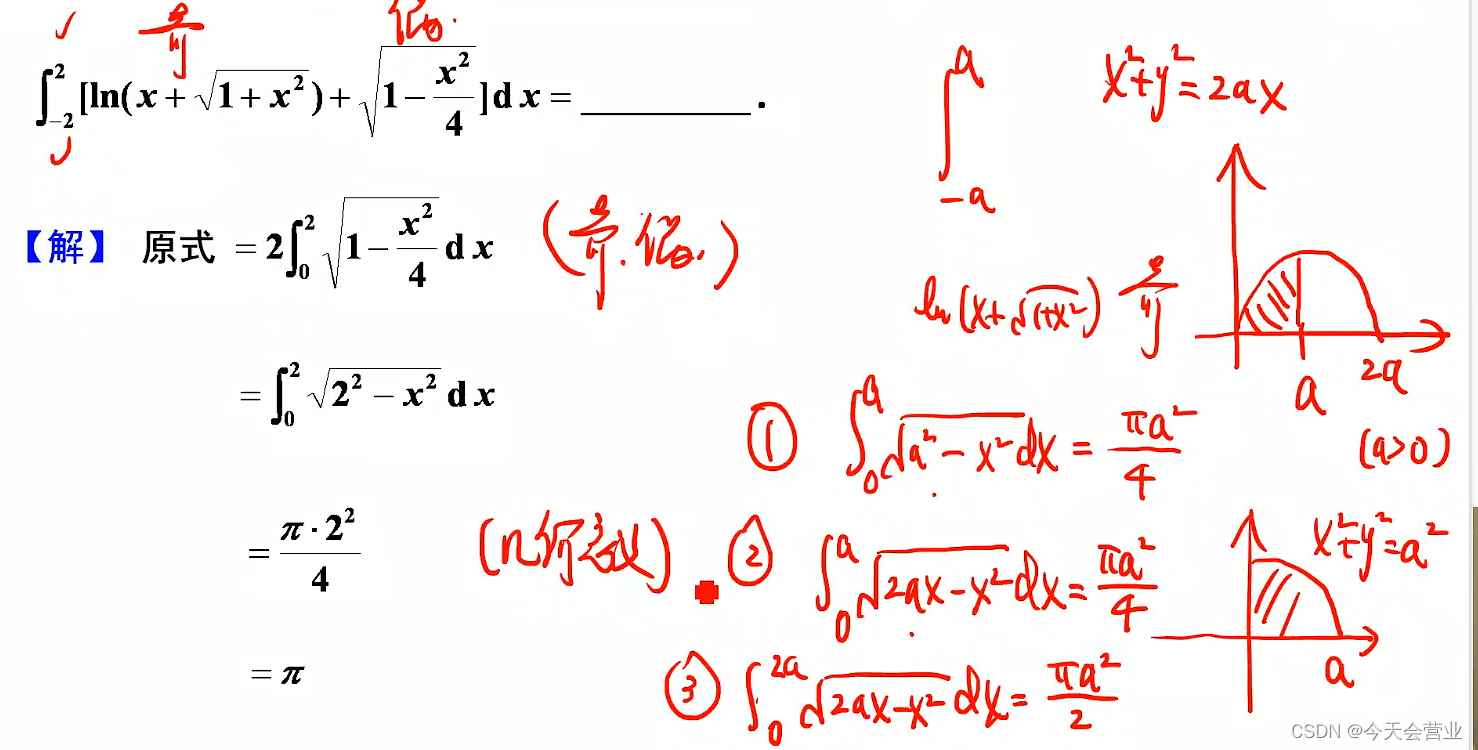
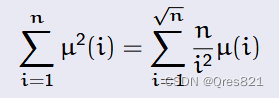


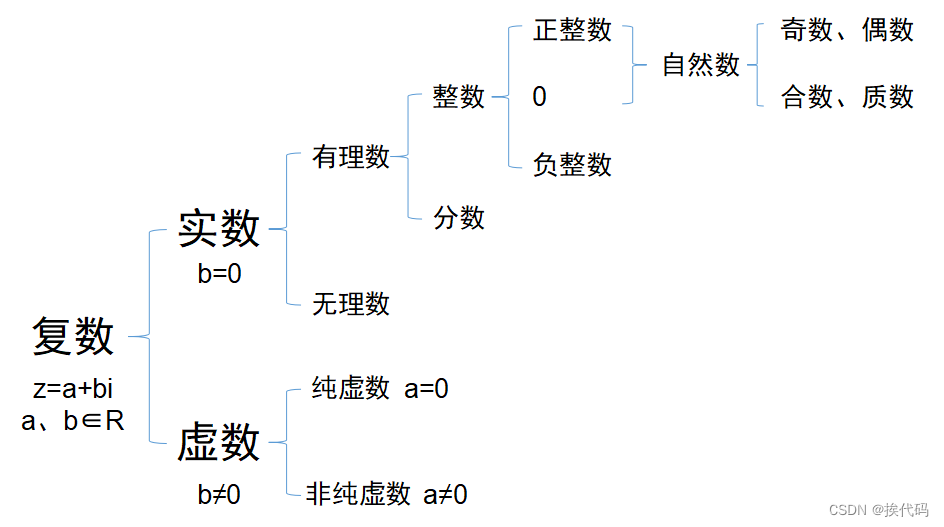




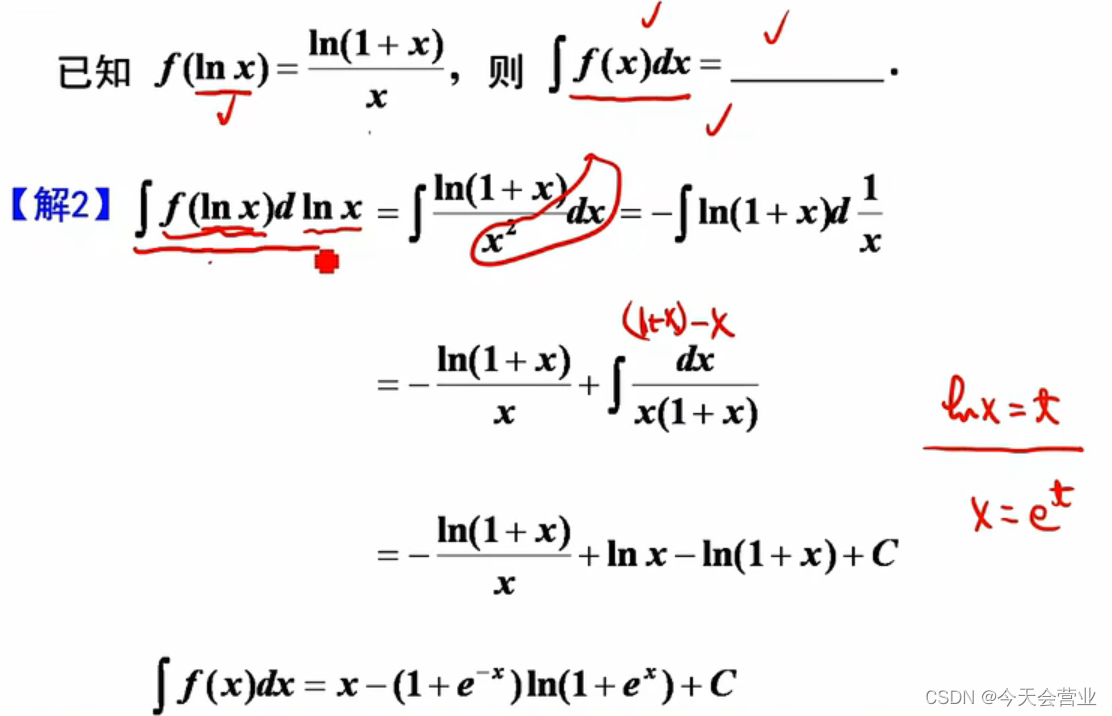
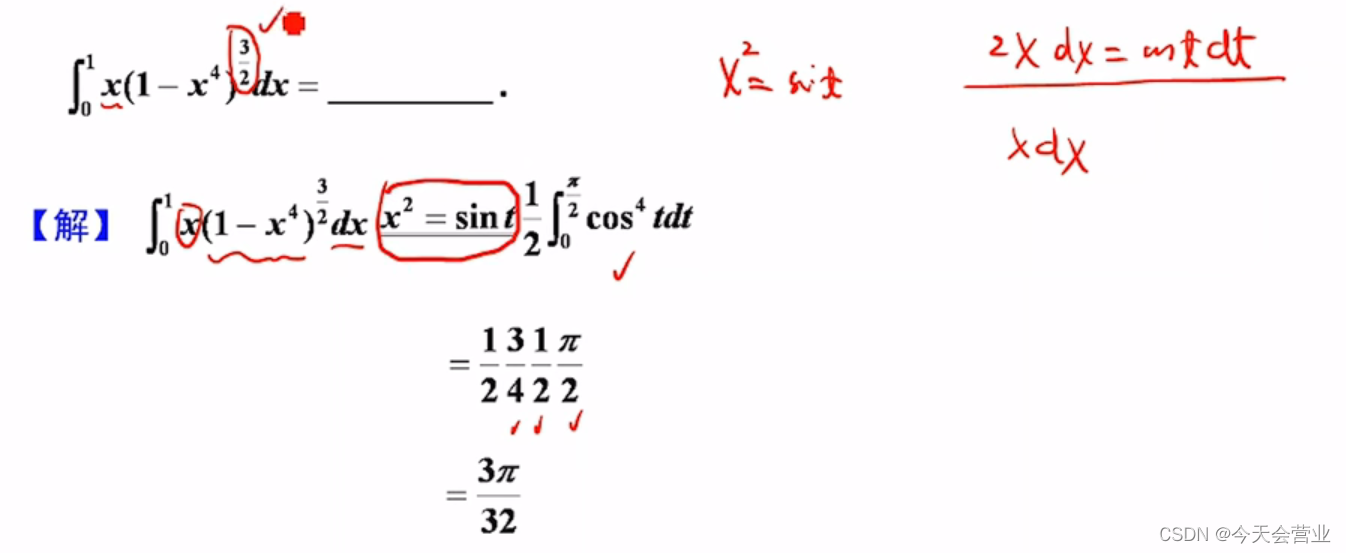

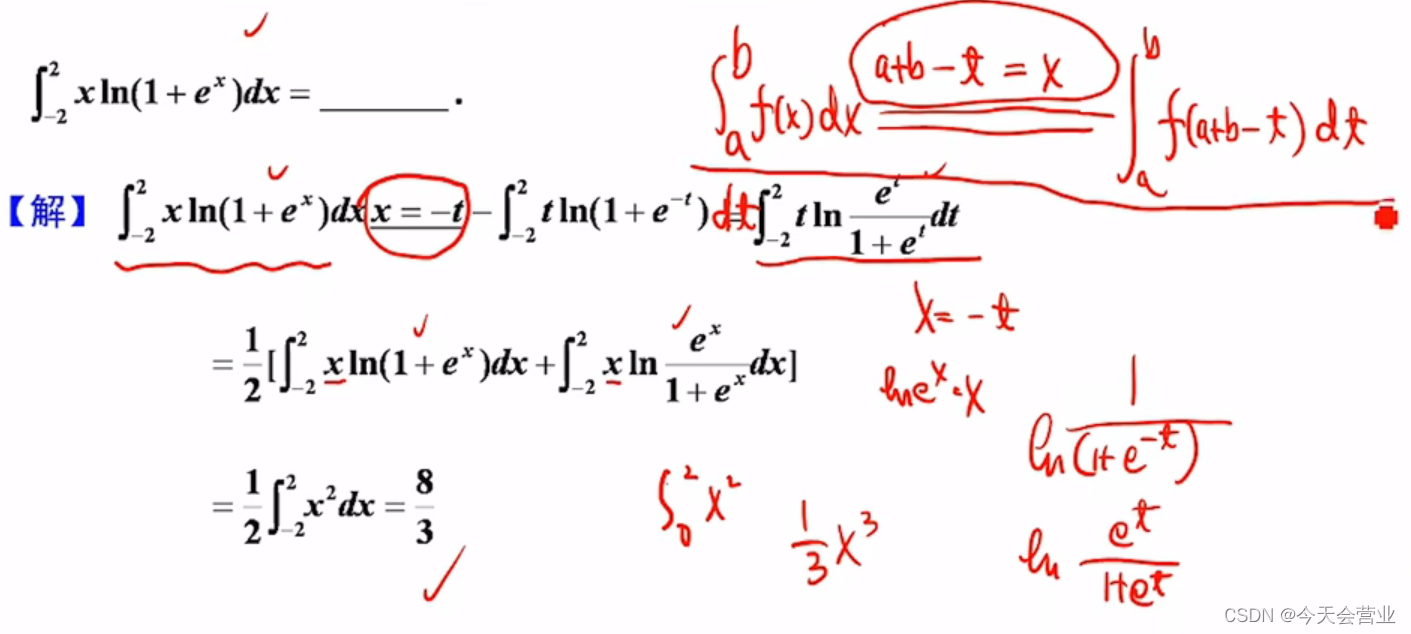












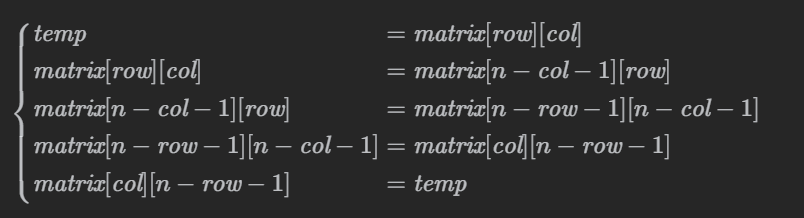






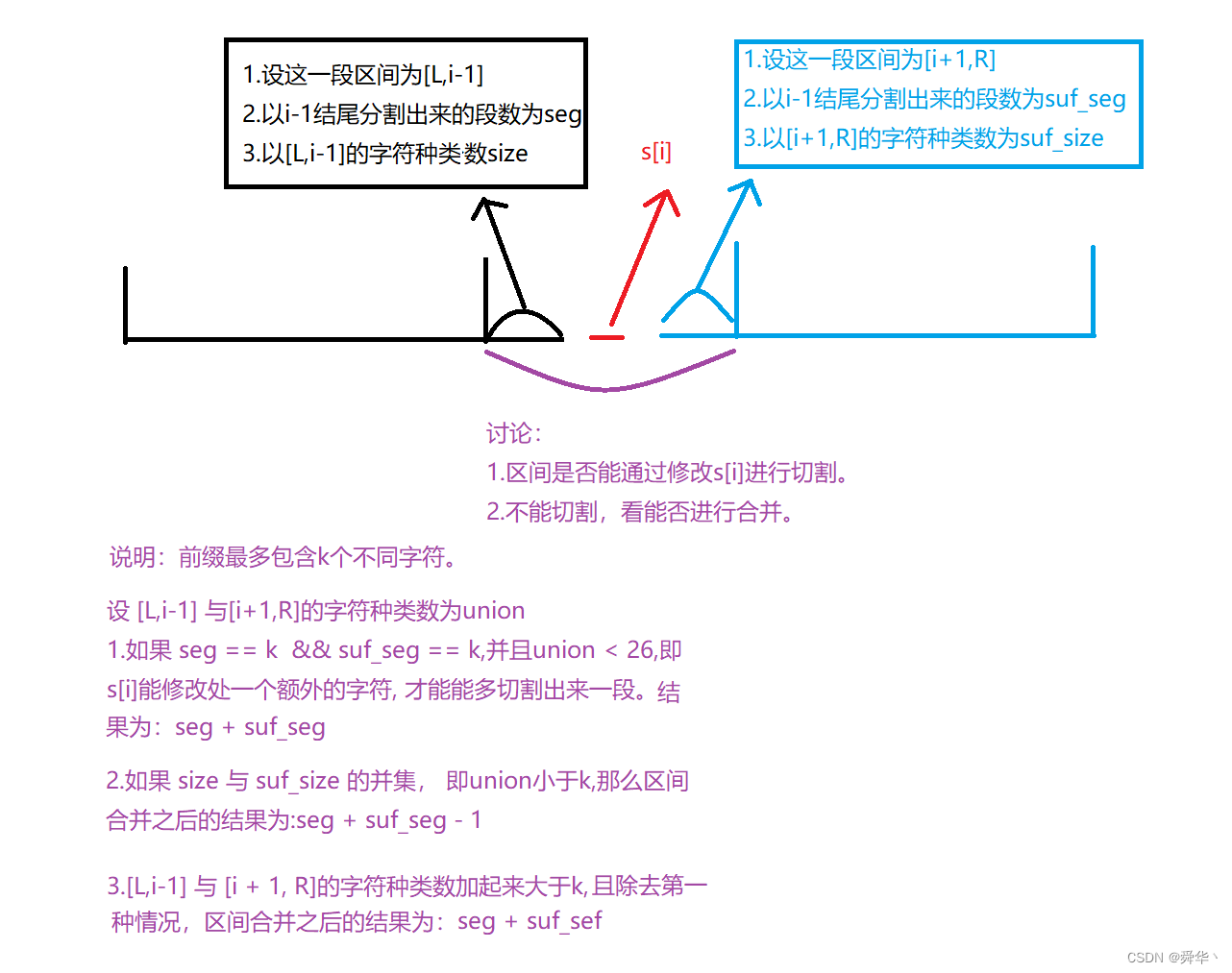
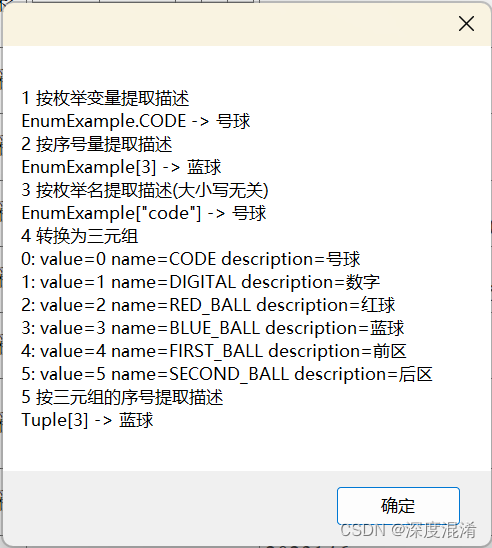
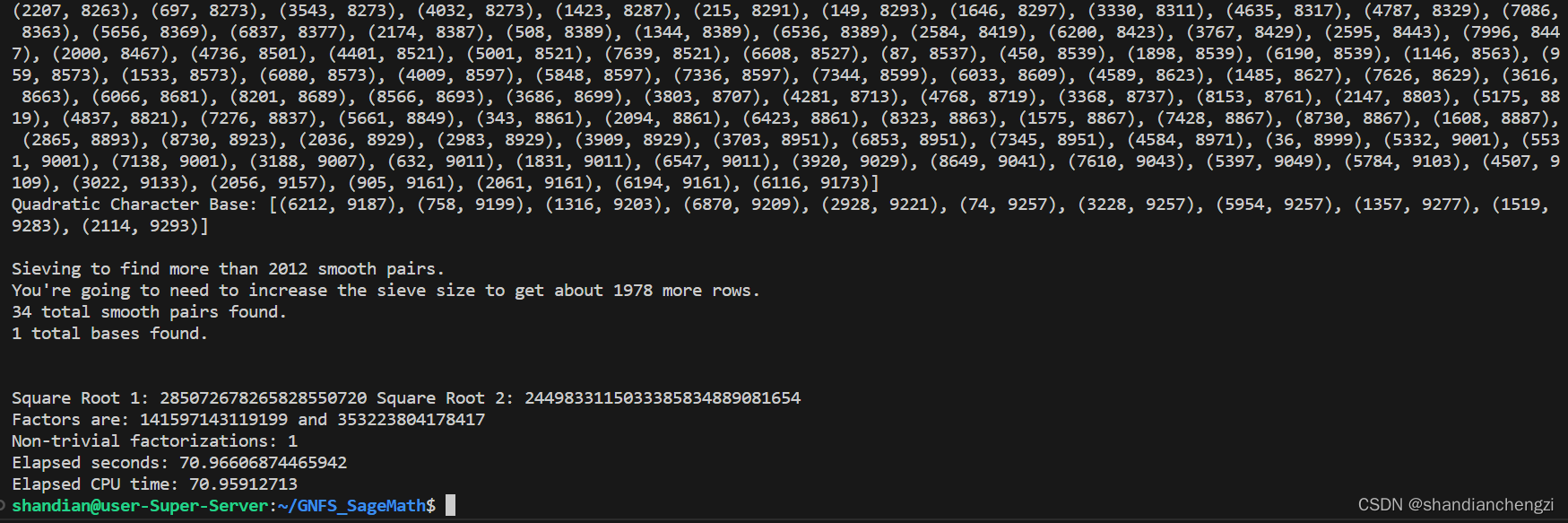
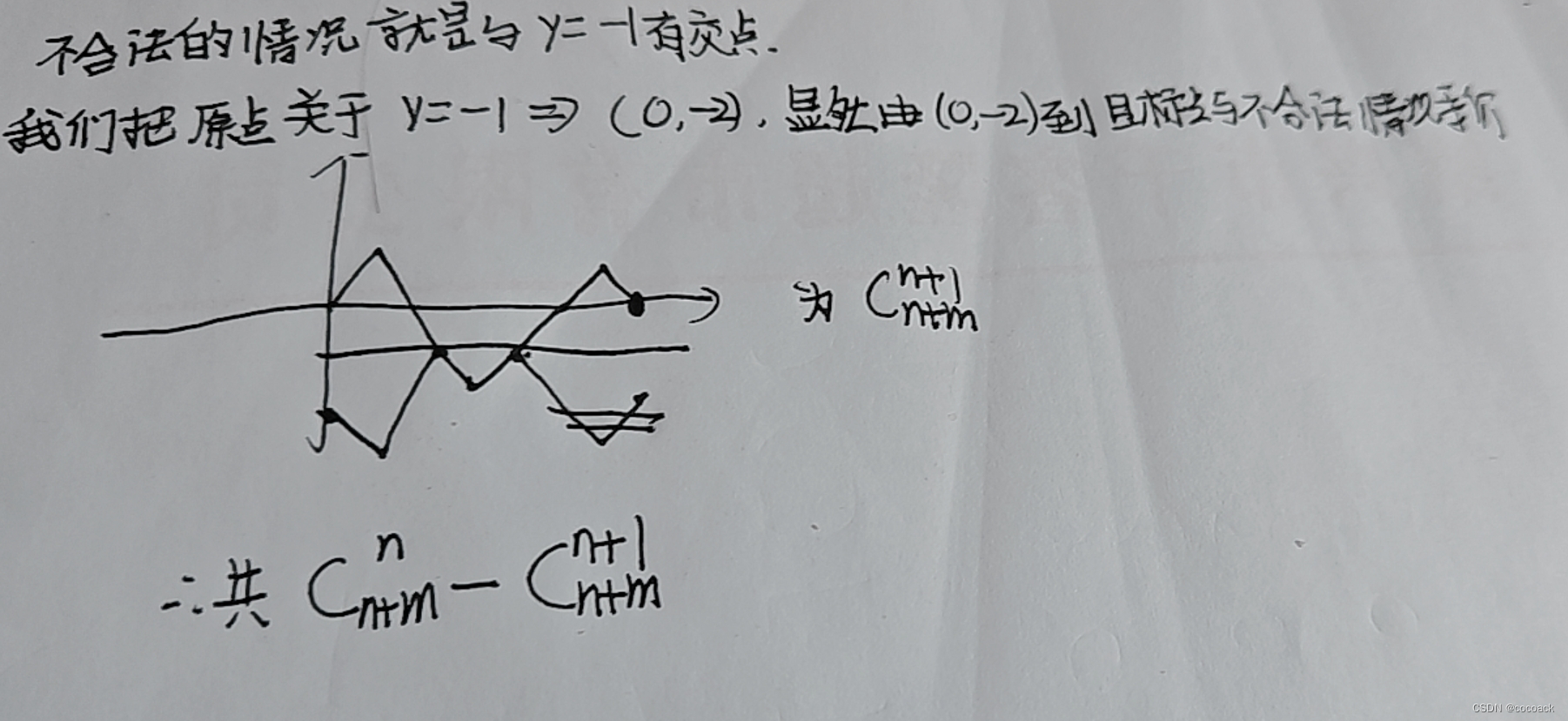



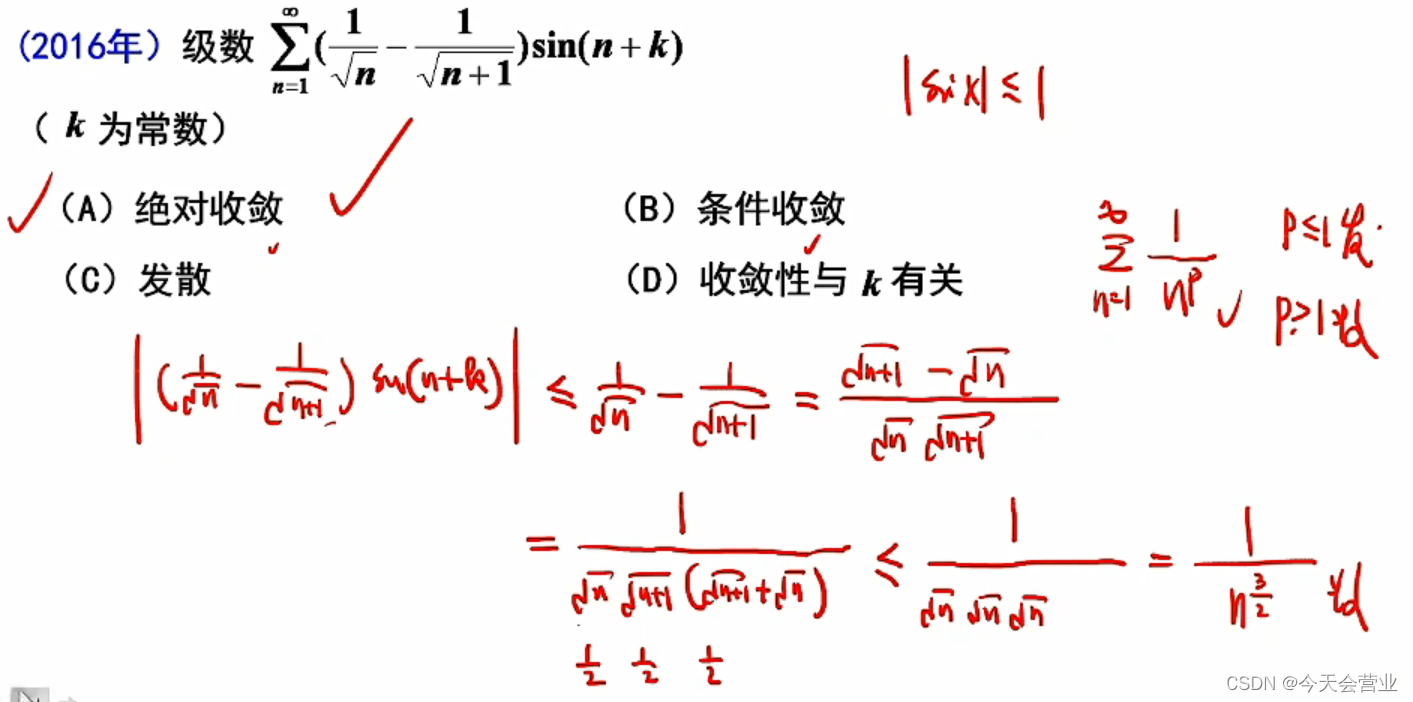
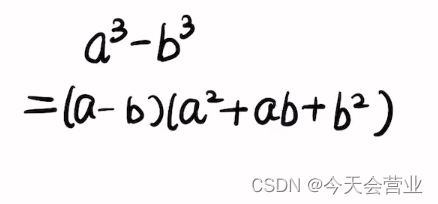









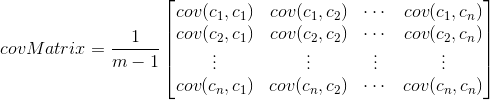








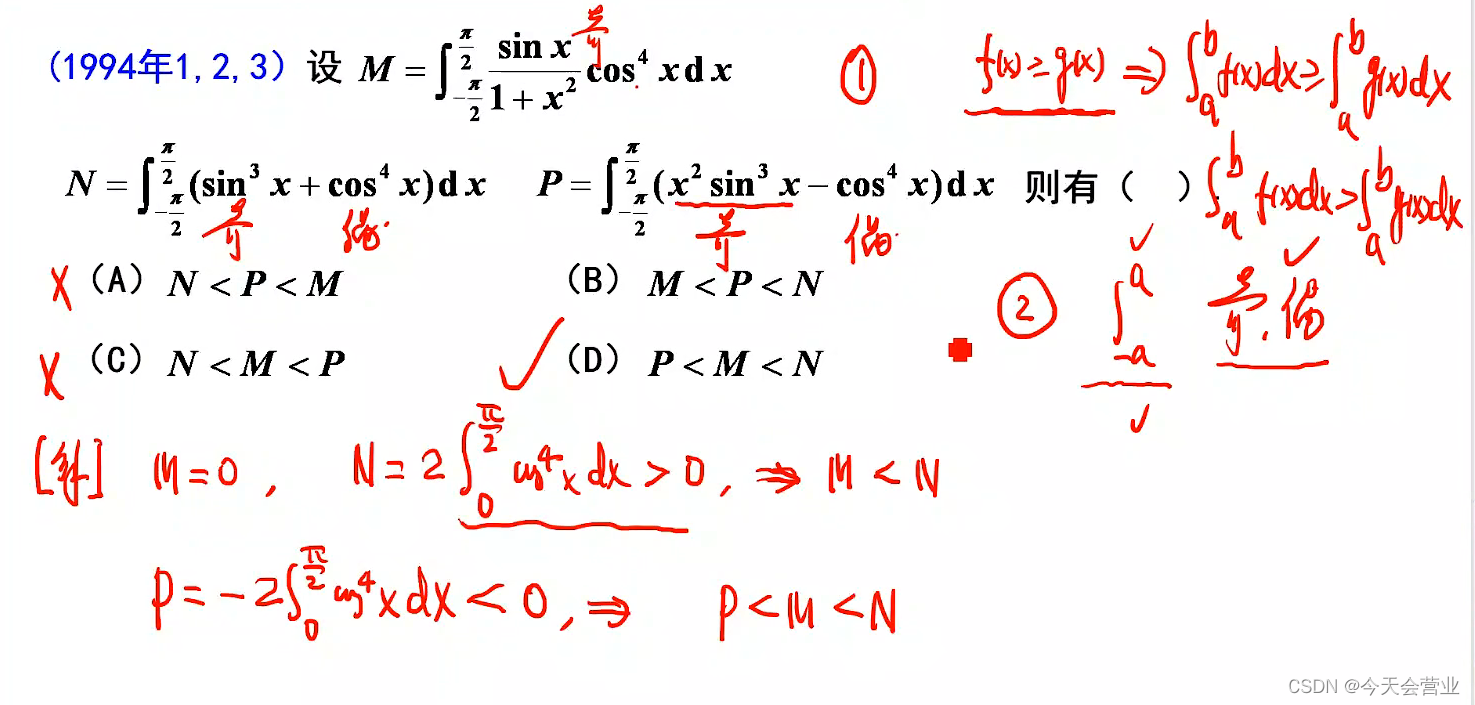



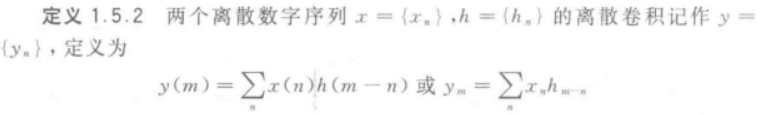



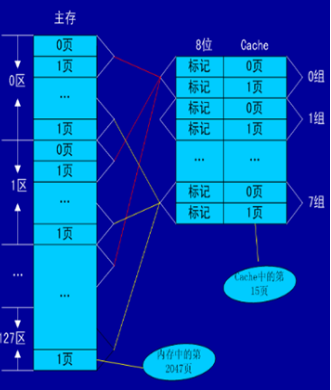



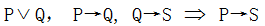
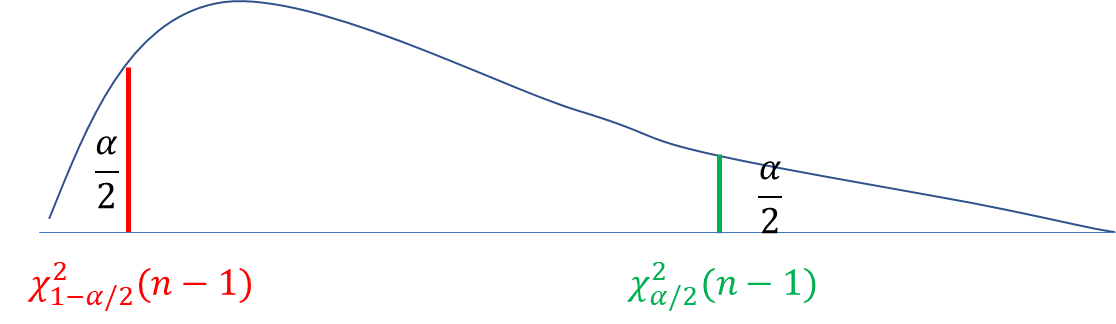


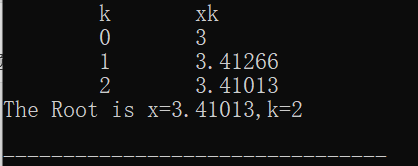







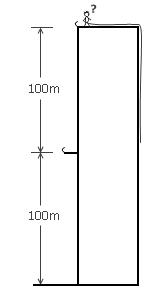







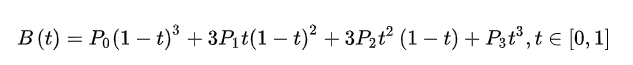



![[NOIP1998 提高组] 车站](https://img-blog.csdnimg.cn/c1b371f1cbb7447f84ad6bf17911aab3.png)





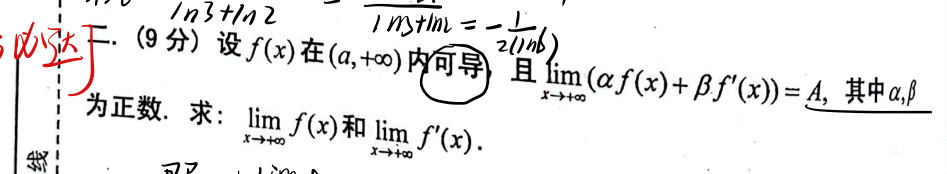

![[Unity基础]游戏中的数学](https://img-blog.csdn.net/20160319134448326)